혹시 파킨슨병(Parkinson's disease)이란 거 들어본 적 있어요? 중추신경계를 침범해서 움직이거나 말하기가 어려워지는 퇴행성질환입니다. 두뇌의 신경세포에 흰자질이 잘못 쌓여서 신경세포가 파괴되면서 생겨나는데, 유명인사 중에 이 병에 걸린 사람이 꽤 있습니다. 히틀러(Adolf Hitler), 마오쩌똥(毛澤東)과 덩샤오핑(登小平), 교황 요한 바오로 2세(John Paul II)가 포함되고, 특히 아직 살아있는 사람 중에는 알리(Muhammad Ali)가 있습니다. [오래 전에 우리나라의 어느 신문에서 알리를 '일개 검둥이 복서'라 부른 황당한 일이 기억나는데 사실 그의 삶은 놀랍지요. 권투선수로서 역사상 가장 뛰어났지만 사상과 삶의 변화는 더욱 놀라운 사람이지요. 이름이 원래 노예를 뜻한 클레이(Cassius Clay), 곧 진흙이었는데 이른바 '일개 검둥이 복서'로 끝날 수 있었을 그를 노예로부터 알리로 만들어준 사람이 말콤엑스(Malcolm X)입니다. 알리의 스승인 셈이지요. 말콤엑스나 알리에 대해서 왜곡되게 배웠거나 또는 아예 들어보지도 못했지요? 우리의 교육환경에서 역사와 사회에 대해 정확한 인식을 가지기가 쉽지 않은 듯합니다.]
아무튼 파킨슨병에 걸리면 흔히 손이 떨리는 증상이 나타납니다. 이 경우에 이른바 뇌자도(magnetoencephalogram; MEG)를 재면 두뇌의 다른 부분 사이에 특징적인 때맞음이 나타난다고 알려져 있습니다. 신경세포는 전기신호로 작동하는데 전류가 흐르면 자기마당이 생겨납니다. 그 자기마당을 측정하면 신경세포들의 활동을 알 수 있으므로 여러 진단의 목적으로 쓸 수 있지요. 아무튼 신경세포들의 거동도 때맞음 현상을 보일 수 있고, 위에서 보기로 든 다양한 계들과 마찬가지로 결합떨개들로서 해석하려는 점이 보편지식을 추구하는 이론과학으로서 물리학의 특성이라 할 수 있겠습니다.
한편 사회경제계(socioeconomic system)에서 널리 알려진 문제로 죄수의 난제(prisoner's dilemma)라는 게임이 있습니다. 어떤 범죄의 두 공범을 잡아서 격리 수용해 놓고 죄를 자백하라고 권유합니다. 둘 다 불지 않고 버티면 무죄로 풀려나게 되고 둘 다 불면 모두 5년형을 받게 되지요. 한편 한 사람만 불고 다른 공범은 불지 않는다면, 불지 않은 사람은 10년형 받고 분 사람은 1년형만 받게 됩니다. 그럴 때 한 공범의 입장에서 자백하는 편이 나을까요, 끝까지 버티는 편이 나을까요?
자연과학이나 공학뿐 아니라 이러한 사회과학에서도 널리 나타나는 문제 중 하나가 최적화(optimization)입니다. 대표적인 것으로 외판원문제(traveling salesperson problem)를 들 수 있지요. 외판원이 서울에 있는 본사에서 가방에 팔 물건을 들고 나와서 대전, 전주, 광주, 목포, 순천, 부산, 울산, 대구, 포항, 강릉 등 전국의 도시를 한 바퀴 돌려 합니다. 그런데 한 번 간 곳은 다시 가면 안 됩니다. 아까 판매한 것을 다시 환불해 달라고 할지 모르니까요. 그러니까 모든 도시를 방문하되 각 도시를 한 번씩만 들러야 하는데 어떻게 하는 것이 가장 짧은 거리로 돌아오는 것일까요? 말하자면 똑똑하게 한 바퀴 도는 방법을 찾자는 것인데, 이를 외판원 문제라고 합니다.
|
아주 명확하고 간단하죠? 이 문제는 사실 여러 가지 다른 문제들과 밀접하게 관련되어 있습니다. 예로서 전기공학에서 고집적회로의 설계나 실생활에서 벽지 자르기를 들 수 있지요. 지물포에 가서 벽지를 살 때 벽지의 무늬를 잘 맞춰서 잘라야 합니다. 잘못하면 버리는 부분이 많게 되지요. 여러 벽에 벽지를 바를 때 벽의 넓이에 따라 여러 크기의 벽지가 필요합니다. 그런데 벽지가 말려있는 두루마리에서 필요한 크기의 벽지를 어떤 순서로 잘라내어야 무늬를 잘 맞추면서 버리는 부분이 가장 적을까 하는 문제가 '벽지 자르기'인데 외판원 문제와 수학적으로 동등합니다. 따라서 어느 하나를 풀면 다른 것도 모두 풀 수 있지요.
이와 동등한 문제를 여러 가지 생각할 수 있는데 그 자체는 간단해 보이지만 사실은 무지무지 어려운 문제입니다. 일반적으로 계의 크기가 커지면 풀이법(algorithm)도 길어지게 마련이지요. 쉬운 문제는 푸는 데 걸리는 시간이 크기에 멱급수(power series)로 주어지는데 이를 다항식시간(polynomial time; P) 문제라 부릅니다. 이러한 다항식시간 풀이법이 알려지지 않은 문제를 미정다항식시간(non-deterministic polynomial time; NP) 문제라고 하지요. 대체로 NP는 다항식시간 풀이법이 존재하지 않고 푸는데 걸리는 시간이 지수적으로(exponentially) 늘어나서 현실적으로 정확하게 풀 수 없다고 생각됩니다. 따라서 NP는 P가 아니라고 믿어지는데, 이는 매우 중요하고 유명한 문제로서 만일 이를 정확히 보이면 역사에 이름이 길이 남을 것입니다. 이러한 NP 문제는 본질적으로 쩔쩔맴을 지닌 복잡계의 전형으로서 물리학, 특히 통계역학의 문제라 할 수 있지요.
|
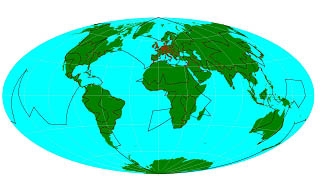
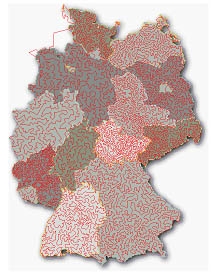
가장 똑똑하게 세계를 일주하는 방법은 무엇일까요? 그림 4는 세계 666개의 도시를 가장 짧은 거리로 일주하는 방법입니다. 서울과 부산도 있고, 북극과 남극도 지나갑니다. 여러분이 나중에 세계 일주를 잘 하려고 해도 이러한 물리를 알아야 되겠네요. 그림 5는 독일을 가장 짧은 거리로 일주하는 방법입니다. 무려 15,112개의 마을을 똑똑하게 도는 방법이니 혹시 독일을 여행할 기회가 있으면 이걸 잘 보고 하면 좋겠네요. 이것이 지금까지 인류가 정확히 푼 가장 커다란 외판원 문제입니다. 푸는 데 얼마나 걸렸는지 정확히는 모르겠으나 초셈틀(슈퍼컴퓨터)를 동원해서 엄청나게 오래 걸렸을 것입니다.
|
자연에는 여러 가지 그물얼개(network)가 많습니다. 예를 들어 우리의 두뇌는 천억 개쯤으로 추산되는 신경세포들이 얽혀서 복잡한 그물얼개를 이루고 있지요. 그런데 이러한 신경그물얼개(neural network)는 어떤 모양을 보일까요? 질서정연하게 규칙적인 모습은 아니지만, 그렇다고 해서 완전히 무질서하게 마구잡이로 있지도 않습니다. 결국 그 사이에서 복잡성을 지니고 있지요.
최근에는 뭇알갱이계를 이러한 그물얼개로 나타내고 그 구조로부터 계의 특성을 알아내려는 시도가 많이 행해졌습니다. 일반적으로 뭇알갱이계에서 구성원과 그들 사이의 상호작용을 각각 꼭지점(마디; node)과 변(연결선; link)으로 나타내면 그물얼개의 구조를 얻게 되지요. 이는 결정(crystal) 등에서처럼 질서가 있는 경우에는 규칙적 그물얼개(regular network), 곧 살창(lattice)이 되며, 완전히 무질서하면 마구잡이 그물얼개(random network)로 주어집니다. 복잡그물얼개(complex network)는 이러한 질서와 무질서 사이에서 복잡성을 보이는 구조를 지녔으며, 그 예로서 신경그물얼개 외에 인터넷 및 웹 연결, 교통 그물얼개, 사회적 관계, 흰자질 상호작용, 신진대사 등이 알려졌습니다.
복잡그물얼개는 일반적으로 각 마디의 연결선 수 또는 연결되어 있는 다른 마디의 수가 서로 달라서 모든 마디가 동등하지 않습니다. 어떤 마디는 연결되어 있는 마디가 매우 많은 경우가 있는데 이러한 마디를 허브(hub)라고 부르며, 이는 마디 중에 당연히 중요한 위치를 차지한다고 할 수 있습니다. 실제로 인터넷 연결이나 항공로, 흰자질 상호작용이나 신진대사 그물얼개들이 이러한 허브 구조를 지닌다고 알려져 있지요. 이러한 경우에 연결선 수에 따른 마디의 분포는 일반적으로 멱법칙(power law)을 따릅니다. 곧 연결선 수가 적은 마디는 많고 연결선 수가 많은 마디는 적은데 마디 수는 연결선 수에 대해서 대수적으로(algebraically) 감소합니다. 이는 바로 고비성을 뜻하지요.
사회적 관계(social relation)도 마찬가지입니다. 예컨대 친구들의 그물얼개를 생각할 수 있지요. 각 사람을 마디, 그들 사이에 친구 관계를 연결선으로 나타내면 그물얼개가 얻어지는데 친구가 특히 많은 사람, 이른바 마당발인 사람이 허브가 되겠지요. 비슷한 예로서 친구 대신에 성관계 상대로 그물얼개를 만들어도 마찬가지입니다. 다시 말해서 영식이는 누구누구랑 잤고 미정이는 누구누구랑 잤는지 엮어보자는 거지요. 그러면 복잡그물얼개를 얻는데, 역시 상대의 수가 많은 사람은 적습니다. 우습고 장난 같은 얘기지만 실제로 ≪네이처≫, ≪사이언스≫ 따위에 나온 논문들이지요.
|
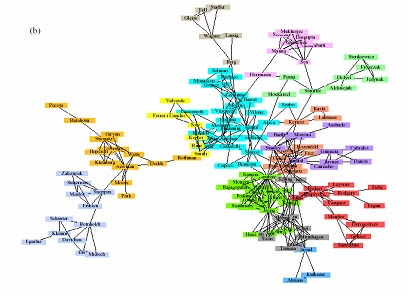
요샌 과학자가 혼자 연구하는 경우는 드물고 보통 여러 사람들이 협동으로 연구를 합니다. 나는 이 사람과 저 사람하고 협동해서 연구했고, 저 사람은 또한 어떤 다른 사람과 협동했고, 이런 식으로 협동한 사람들끼리 연결할 수 있겠지요. 그림 6은 복잡그물얼개 분야에서 각 연구자를 마디로 하고 협동연구자끼리 연결선을 그어서 만든 그물얼개를 보여줍니다. 오른쪽 아래에 우리나라의 연구자들도 몇 사람 볼 수 있습니다. (제 이름도 들어있지요.)
경제계도 역시 복잡계라 할 수 있으며, 이러한 관점에서 경제계를 다룬 책들이 있습니다. 물리, 수학, 화학, 생물, 사회과학, 그리고 예술 등 여러 분야의 전문가가 모여서 복잡계 연구를 수행하는 산타페 연구소(Santa Fe Institute)가 널리 알려져 있는데 여기에서 펴낸 ≪전개하는 복잡계로서의 경제(The Economy as an Evolving Complex System)≫라는 책이 있지요. 유명한 경제학자인 크루그먼이 복잡계 관점에서 쓴 ≪스스로 짜이는 경제≫는 앞에서 언급했습니다.
이제까지 물리와 생물, 공학, 그리고 사회과학 따위 여러 분야에서 복잡계의 예를 몇 가지 들었습니다. 이렇듯 여러 분야에서 매우 다양하게 나타나는데 그 가운데에서 어떤 보편성을 찾아내고, 이에 따라 다양한 현상을 하나의 틀로 해석하려 합니다. 이른바 보편지식 체계를 구축하고자 노력하지요. 이것이 바로 물리학의 독자성이라 할 수 있습니다.
일반적으로 물리학은 보편지식 체계를 추구하므로 복잡한 현상은 다룰 수 없다는 것이 기존의 생각이었습니다. 비교적 간단한 현상들만 보편지식 체계로 해석할 수 있고, 반면에 복잡한 현상, 예를 들어 생명과 인간이나 사회현상은 보편지식 체계를 구축할 수 없다고 생각했지요. 그런데 20세기 후반에 물리학의 방법이 정립되면서 부분적으로 '간단한' 복잡계 현상은 해석할 수 있게 되었습니다. 이에 힘을 얻어서 일반적인 복잡계에 대해서 보편지식 체계를 구축하려는 시도가 시작되었다고 할 수 있습니다. 따라서 복잡계는 21세기 물리학의 핵심적인 연구 주제로 자리매김하리라 예상합니다. 이는 물리학의 지평을 크게 넓히고 생명을 비롯한 자연에 대한 새로운 해석을 얻는데 기여할 것입니다.
* 이 연재기사는 지난 2008년 12월 '최무영 교수의 물리학 강의'라는 제목의 책으로(책갈피 출판사) 출판되었습니다



전체댓글 0