
|
그림 2는 해안선을 보여줍니다. 파란 부분이 바다인데 위의 왼쪽 그림을 보면 가운데 조그마한 반도가 하나 있죠? 하얀 선의 네모로 표시했는데 이를 확대해서 화살표를 따라 오른쪽 그림에 나타내었습니다. 반도가 크게 보이네요. 그런데 반도 남동쪽에 만이 있는데 이걸 또 확대해서 화살표를 따라 옆 그림에 나타내었습니다. 만이 크게 보이고 가운데 조그마한 호수가 하나 있네요. 이 호수를 확대해서 화살표를 따라 아래 그림에 보였습니다. 호수가 크게 보이는데 석호인 듯하네요. 우리나라 속초에 널리 알려진 석호가 둘 있었죠? 청초호와 영랑호로, 아름다웠는데 안타깝게도 시궁창이 돼 버렸더군요. 요새는 좀 나아졌으리라 기대해 봅니다. 아무튼 석호를 확대해 보니 그 안에 조그마한 반도가 하나 있네요. 요걸 또 확대했더니 반도가 커졌죠. 반도의 부분을 다시 확대했더니 조그만 반도가 또 있는 것이 보입니다. 그런데 처음 시작한 그림으로 다시 돌아왔어요. 끝없이 돌게 되네요. 이렇듯 공간에서 '스스로 닮음' 구조를 지닌 대상을 쪽거리라고 합니다.
그런데 이러한 해안선 그림에서는 눈금이 얼마인지 알 수 없습니다. 예컨대 위 왼쪽 그림에서 반도를 표시한 네모의 한 변 길이가 10 미터인지, 1킬로미터인지, 또는 100 킬로미터인지 알 수가 없죠. 왜냐하면 점점 확대하면 다시 돌아오니까 주어진 그림이 어떤 단계인지 알 수 없기 때문이지요. 우리나라 남서해안에 이렇게 복잡한 해안선의 지도를 보면 그 눈금이 어느 크기인지 해안선만 보아서는 알 수 없습니다. 이러한 성질을 눈금불변(scale invariant)이라고 표현합니다.

|

|

|
그림 3은 인공위성에서 찍은 히말라야 빙하의 모습인데, 이것도 역시 어느 한 부분을 확대해 보면 전체 모양이 비슷하게 들어 있죠. 그림 4는 번개의 사진입니다. 이것 역시 한 부분을 확대해 보면 전체 모양이 다시 들어있네요. 그림 5는 브로콜리의 한 품종입니다. 튀어나온 돌기 하나를 떼어내어 확대해 보면 전체 모양을 다시 볼 수 있어요. 자연은 할 수 있는 것은 잘 이용하지요. 그밖에도 콩팥의 세뇨관이나 허파꽈리, 물건이 찢어지는 모양, 눈송이, 달의 분화구 등에서 스스로 닮은꼴이 알려져 있습니다.
|
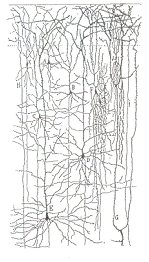
그림 6은 우리 두뇌 피질(cortex)의 조직으로 신경세포들이 모인 신경그물얼개(neural network)를 보여줍니다. 신경세포는 세포체(cell body)와 액손(axon)이라고 부르는 긴 줄기로 되어 있고. 액손의 끝은 시냅스(synapse)를 통해 다른 신경세포와 연결돼 있습니다. 세포체에는 나무줄기형태 돌기(dendrite)로 많이 갈래가 쳐있는데 그들은 다른 신경세포들과 시냅스로 연결돼 있지요. 그래서 신경세포들은 매우 많은 수가 복잡하게 그물얼개를 이루며 얽혀있습니다. 우리 두뇌에는 신경세포가 몇 개쯤 있는지 알아요? 대략 수백억에서 천억 개 정도라고 하며, 각 세포는 평균적으로 수만 개가량의 다른 세포들과 연결되어 있다고 하지요. 아무튼 신경세포들이 복잡하게 다른 세포들과 연결돼 있는 그물얼개도 어느 정도 스스로 닮은 쪽거리 구조를 가지고 있습니다.
앞에서 공간의 차원에 대해 논의했지요. 선이라는 대상은 1차원, 면은 2차원, 공간은 3차원, 상대론에서 시공간은 4차원 등을 알고 있지요. 그런데 쪽거리라는 대상은 놀랍게도 차원이 자연수가 아니라 일반적으로 소수입니다. 예컨대 1.5차원이나 2.3차원일 수 있습니다. 그러니까 남서해안선처럼 쪽거리 해안선은 어떤 눈금의 자로 재느냐에 따라 길이가 다르게 됩니다. 사실 세밀한 자로 잴수록 길이가 길어지게 되지요. 이러한 쪽거리 선은 물론 면은 아니므로 2차원보다 작지만 보통의 선과 달라서 1차원보다는 크다고 할 수 있습니다. 자세한 논의는 하지 않지만 대체로 차원이란 길이가 2배가 될 때 양이 몇 배로 늘어나는가에 따라 정의할 수 있습니다. 면의 넓이는 네 배, 곧 22으로 늘어나므로 2차원이고 공간의 부피는 여덟 배, 곧 23으로 늘어나니까 3차원이지요. 일반적으로 d 차원에서는 2d 로 늘어나는데 쪽거리에서는 d 가 소수로 주어집니다.
예로서 고양이의 시각피질에서 신경세포들로 이루어진 신경그물얼개는 1.7차원이라고 알려져 있습니다. 그런데 시험관에서 인공수정을 통해 고양이를 만들면 시각피질의 신경그물얼개 차원이 1.4 정도로 줄어든다고 합니다. 자연스러운 상태 보다는 발달이 떨어진다는 뜻이겠지요. 아무래도 인공적인 조작은 자연과 똑같기 어렵고, 어쩌면 위험할 수도 있음을 암시하는 것이 아닐까요?
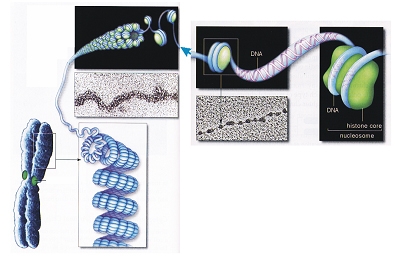
유전정보를 가지고 있는 디옥시리보핵산(DNA)은 세포핵의 염색체(chromosome)에 있다는 것 모두 알지요? 염색체에서 DNA를 어떻게 꾸리고 있는지 그림 7에 보였습니다. 왼쪽 아래에 염색체가 있지요. 그 일부를 확대해보면 DNA가 똘똘 말려있는데, 그 말려 있는 뭉치를 확대해보면 그 부분부분이 또 똘똘 말려있네요. 똘똘 말고, 또 말고, 또 말고, 계속되어서 스스로 닮은 쪽거리 구조를 가지고 있습니다.
|
사람의 세포 하나의 크기가 얼마 쯤 되죠? 대략 10-5 m, 그러니까 0.01 mm 또는 10 마이크로미터 정도인가요? 그 안에 세포핵은 그것의 10분의 1이고, 세포핵 안에 염색체는 훨씬 작아서 10억분의 1 미터밖에 되지 않습니다. 그런데 그 염색체 안에 들어있는 DNA를 쫙 풀면 놀랍게도 1.8 미터가 됩니다. 이 정도 길지 않으면 우리 몸의 정보를 다 넣을 수 없겠지요. 이를 무려 10억분의 1로 줄여서 집어넣으려면 이렇게 스스로 닮은 쪽거리 구조를 가질 수밖에 없겠지요. 그리고 이는 사실 DNA와 실패 역할을 하는 흰자질 사이의 전기력 때문에 가능합니다. 미묘한 생명현상도 결국 물리법칙을 따라 짜여 있네요.
DNA는 정보를 어떻게 저장하고 있지요? DNA는 A, C, T, G로 표시하는 아데닌(adenine), 시토신(cytosine), 티민(thymine), 구아닌(guanine)의 네 가지 염기로 이루어져 있습니다. 그 네 가지가 어떤 순서로 배열되어 있느냐에 따라서 정보가 정해지는 겁니다.
여러분 진법이라는 것 다 배웠죠? 우리가 일상에서 쓰는 것은 10진법입니다. 왜 하필 10진법을 쓰겠습니까? 글쎄요, 아마도 우리 손가락이 10개라서 그런 것인지도 모르겠습니다. 10 손가락 다 세면 하나 올라가게 되니까요. 원리적으로 더 편리한 것은 2진법이겠네요. 간단히 2개만 가지고 모두 표현할 수 있으니까요. 그래서 컴퓨터에서는 2진법을 씁니다. 그런데 생체계에서는 DNA에 정보를 저장할 때 A, C, T, G를 가지고 4진법을 씁니다. 한편 흰자질은 20가지의 아미노산amino acid을 적절한 순서로 연결해서 만들어지니 20진법을 쓰는 셈이지요.
|
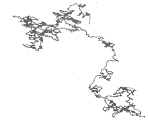
아무튼 DNA에서는 이 네 가지 염기가 어떤 순서로 배열되는가에 따라 여러 가지 정보를 저장합니다. 당연한 얘기지만 그것을 규칙적으로 배열하면 별 의미가 없습니다. 저장된 정보는 매우 빈약한 것이지요. 대신에 마구잡이로 배열해도 의미가 없고 적절히 복잡하게 배열해야 많은 정보를 저장할 수 있습니다. 네 가지 염기를 평면에서 네 방향에 대응시키면 DNA의 염기 서열을 평면에서 걷기로 나타낼 수 있습니다. 그림 8은 이러한 방법으로 박테리아의 염기 서열을 걷기로 나타낸 것인데 복잡하네요. 한 부분을 확대해 보면 전체 모양이 비슷하게 나타나는 스스로 닮은꼴을 보이지요. (이른바 complicated가 아니라 complex 입니다.) 차원이 1.5에서 1.7인 쪽거리라고 할 수 있습니다. 아무튼 많은 정보를 저장하려면 복잡해야 한다는 이야기입니다.
그밖에 사회현상에서 스스로 닮은 쪽거리 구조를 보이는 예로서 도시가 자라는 모습이 알려져 있습니다. 대도시에서 시가지가 자라는 모습에서 한 부분을 확대해보면 대략 전체 모양이 들어있다는 말이지요.

|
예술에서 스스로 닮은 쪽거리 구조를 표현한 작품으로 에셔의 판화는 이미 앞에서 소개했습니다. 리만기하학과 닫힌 우주를 표현하는 12강 그림 17의 ≪더 작게 더 작게≫에서 가운데 부분을 확대해보면 전체가 그대로 들어있지요. 그림 9는 호킨슨(Tim Hawkinson)의 작품으로 제목이 없습니다. 이른바 ≪제목 없음≫이 제목이지요. 왼쪽 그림의 부분을 확대해서 오른쪽에 보였습니다. 스스로 닮음이 잘 나타나 있네요.

|
그림 10은 ≪복잡성 연구≫라는 작품입니다. 김주현 작가의 작품으로 왼쪽은 도면, 오른쪽은 완성된 작품의 사진인데 스스로 닮음에서 더 나아가 떠오름까지 예술로서 나타낸 보기 드문 시도인 듯합니다. 상당히 적절한 표현이고 정확한 느낌을 주네요. 제목에 걸맞다고 생각합니다.
* 이 연재기사는 지난 2008년 12월 '최무영 교수의 물리학 강의'라는 제목의 책으로(책갈피 출판사) 출판되었습니다



전체댓글 0