비유하자면 1천 층짜리 건물이 있는데 그 지하 10층 바닥에 개미가 한 마리 있어요. 물론 지하실이라서 빛은 전혀 없죠. 개미가 거기서, 과연 이 건물이 어떻게 생겼을까 하고 추측하는 것보다 인간이 우주의 모습을 알아내는 것이 더 어렵다고 할 수도 있습니다. 크기를 비교하면 개미와 천 층짜리 건물보다 인간과 우주의 차이가 훨씬 더 크기 때문이지요. 사실 인간이 우주를 어떻게 이해할 수 있을지, 그것이 과연 가능할지는 수수께끼 같은 문제입니다.
그럼에도 불구하고 인간은 우주를 제법 잘 이해하고 있다고 믿어집니다. 그래서 아인슈타인은 "우주에 대해 가장 이해할 수 없는 점은 우주가 인간에게 이해되어진다는 사실이다"라고 말했지요. 역설적인 표현이지만 공감이 가는 지적입니다. 우주의 규모에서 보면, 사실 우리 은하 하나 정도 없어지는 건 아무런 영향도 없다고 할 수 있지요. 그러나 우리 은하에서 보면 태양계는 먼지 한 조각만도 못하고, 지구 정도는 새삼 말할 필요도 없습니다. 우주의 눈금에서 볼 때 인간은 보잘 것 없이 너무나 하찮은 존재이고 아무런 의미도 없어 보이지요. 그러나 이러한 인간이 우주를 해석하고 이해하려고 노력하고 있고, 또한 상당한 이해에 도달해 있다는 겁니다. 참으로 놀라운 일이라 하지 않을 수 없습니다.
천체의 거리 측정
먼저 천체까지의 거리를 어떻게 재는지 생각해 보겠습니다. 밤하늘의 별이 얼마나 멀리 떨어져 있는지 생각해 보자는 건데 우리 모두 어렸을 때 한번쯤 가져보던 의문이지요. 천체까지의 거리를 측정하는 방법은 여러 가지 있는데 그 중 가까운 천체의 거리를 잴 때에는 간단하게 시차(parallax)를 조사하면 되고, 이보다 조금 먼 천체의 경우에는 별의 밝기를 이용할 수 있습니다. 멀리 떨어져 있는 천체의 경우에는 빨강치우침을 이용하지요.
|
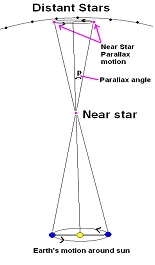
별의 시차(stellar parallax)를 그림 1에 나타내었습니다. 지구는 해 주위를 돕니다. 공전 자리길 면에 수직 방향으로 가까운 곳에 별이 하나 있다고 할까요. 그림에서 지구가 해의 왼쪽에 있을 때 이 별을 관측하면 별은 멀리 떨어진 별을 기준으로 해서 그 오른쪽에 있는 걸로 보입니다. 그런데 6개월을 기다려서 지구가 해의 오른쪽에 오면 가까운 별은 멀리 있는 기준 별의 왼쪽에 있는 것으로 보이네요. 그러니까 가까운 곳에 있는 별을 관측하고 6개월 있다가 다시 관측하면 그 위치가 바뀐 걸로 나타납니다. 이 경우에 별은 실제로는 정지해 있지만 지구의 공전 때문에 움직이는 것으로 보이는데, 이렇게 한 해에 걸쳐 별이 보이는 방향이 달라지는 차이를 연주시차(annual parallax)라고 합니다. 그림 1에 보였듯이 기준 별에 대해 보이는 방향의 각도 변화로 나타내지요.
이 시차는 실제로는 매우 작습니다. 왜냐면 그림에서 지구와 태양 사이의 거리는 1 AU인 1억 5천만 킬로미터인데 별까지의 거리는 훨씬 크지요. 가장 가까운 별인 프록시마만 하더라도 4.2광년이니 무려 40조 킬로미터입니다. 빛이 걸리는 시간으로 비교해보면 8분 19초와 4.2년이니 시차가 얼마나 될지 짐작이 가죠. 각도 1초("), 곧 3600분의 1도도 안 됩니다. 간단한 삼각함수 계산을 해보면 가장 큰 프록시마의 경우에도 0.77" 밖에 되지 않지요. 따라서 연주시차를 이용해서 거리를 잴 수 있는 별은 태양계에 매우 가까운 별에 국한되어 있습니다. 거리가 50광년만 돼도 시차는 워낙 작아서 재기 어렵지요. 연주시차가 1"에 해당하는 거리를 1파세크(pc; parsec)라고 하는데 3.26광년 쯤 됩니다. 곧 1 pc ≒ 3.26 ly ≒ 3.1×1016 m, 대략 30조 킬로미터라 할 수 있습니다.
다음은 별의 밝기를 이용하는 방법입니다. 별을 밝기에 따라 등급을 매겨서 밝은 별부터 1등성, 2등성, 3등성 등으로 부릅니다. 이는 로그눈금으로서 원래 1등성이 6등성의 100배 밝도록 정의하였으므로 등급이 하나 올라가면 2.5배가량 밝아지게 되지요. 해는 밤하늘의 어떤 별보다도 엄청 밝아서 대략 -27등급입니다. 그러니 1등성보다도 1000억 배 이상 밝은데 이는 해가 실제로 이처럼 밝아서가 아니라 워낙 가까이 있기 때문입니다. 다른 별은 해보다 훨씬 멀리 있어서 어두워 보이는 거지요. 흐릿한 별 가운데에서도 실제로는 해보다 훨씬 밝은 별이 많습니다. 워낙 멀어서 어두워 보이는 것뿐이지요. 우리에게 보이는 밝기에 따라 매긴 등급을 겉보기등급(apparent magnitude)이라 부릅니다.
따라서 별의 실제 밝기를 비교하려면 모든 별이 같은 거리에 놓여있다고 가정하고 등급을 매겨야 합니다. 보통 10 pc, 대략 33 ly 쯤 떨어져 있을 때를 기준으로 하며 이를 절대등급(absolute magnitude)이라 하지요. 올베르의 역설에서 논의했듯이 별이 우리로부터 멀어지면 거리의 제곱에 반비례해서 (겉보기)밝기가 떨어집니다. 따라서 별의 겉보기등급을 절대등급과 비교하면 그 별의 거리를 쉽게 알 수 있지요.
별의 겉보기등급을 알려면 밤하늘에서 바로 밝기를 측정하면 됩니다. 그러면 절대등급을 어떻게 알 수 있느냐 하는 문제가 남네요. 이를 추정하는 데는 몇 가지 판단기준이 있습니다. 한 가지 방법으로는 많은 별들이 밝기와 빛깔이 관련되어 있다는 사실을 이용합니다. 이른바 검정체 내비침에서 지적했듯이 온도가 높을수록 짧은 파길이의 빛을 내비치므로 별 빛깔을 보면 그 온도와 실제 밝기, 곧 절대등급을 짐작할 수 있습니다. 예를 들어 빨간 별 보다는 노란 별, 그보다는 흰 별, 그리고 파란 별이 온도가 높고 따라서 같은 크기면 더 밝지요. 해는 무슨 빛깔이지요? 대체로 노랑과 주황빛으로 파길이가 긴 편이니 온도가 그리 높은 편이 아니고 밝기도 시원찮다는 얘기네요.
그리고 별무리에 시피이드변광성이 포함되어 있으면 이를 이용해서 별무리까지 거리를 잴 수도 있습니다. 밝았다 어두웠다 밝기가 변하는 별을 변광성이라 하는데 이중성을 9강에서 언급했지만 진정한 뜻에서 변광성은 시피이드변광성을 말합니다. 별이 불안정해서 염통이 맥박 치듯이 커졌다 작아졌다 진동하므로 맥동변광성이라 부르지요. 별이 부풀면 밝아지고 줄어들면 어두워지므로 밝기가 주기적으로 변합니다. 그런데 이러한 맥동변광성의 주기는 그 밝기와 관련되어 있습니다. 따라서 관측을 통해 주기를 재면 그 별의 밝기, 곧 절대등급을 알 수 있고 이를 겉보기등급과 비교하면 얼마나 멀리 있는지 쉽게 알 수 있어요.
대부분의 외계은하처럼 아주 멀리 떨어져 있는 천체는 이런 방법으로도 거리를 잴 수 없습니다. 워낙 멀리 있으면 은하에서 별 하나하나를 볼 수 없고 은하 전체가 마치 별 하나처럼 보이지요. 이런 경우에는 앞 강의에서 언급한 빨강치우침을 이용합니다. 은하에서 나온 빛을 분석해서 빛띠가 빨강 쪽으로 얼마나 치우쳤는지 보면 은하가 우리에게서 얼마나 빨리 멀어지고 있는지 알 수 있습니다. 그런데 은하가 멀어지는 빠르기 v와 그 은하까지 거리 r은 서로 비례해서 이미 언급한 허블의 법칙
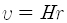
|
이 성립함이 알려져 있습니다. 비례상수 H는 허블상수(Hubble constant)라 부르며, 현재 받아들여지는 값은 71 km/s·Mpc 정도입니다. 따라서 태양계로부터 1 Mpc (≡ 106 pc, 대략 300백만 광년) 떨어져 있는 은하는 초마다 71 킬로미터씩 우리로부터 멀어지고 있습니다.
관측을 통해 빨강치우침을 재면 은하가 멀어지는 빠르기를 알 수 있고, 여기에 허블의 법칙을 이용하면 거리를 바로 얻을 수 있습니다. 빨강치우침의 크기 z는 원래 파길이
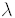
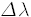
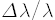
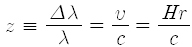
|
가 얻어집니다. 이 관계로부터 은하까지의 거리 r을 구할 수 있겠네요.



전체댓글 0