열(heat)은 언제나 뜨거운 곳에서 차가운 데로 흘러가지요. 이는 열역학 둘째 법칙의 예로서 널리 알려진 현상입니다. 열이란 에너지가 전달되는 방식의 하나로서 일work과 대비됩니다. 즉 어떤 계에서 에너지가 다른 계로 전달되는 방식에는 일과 열의 두 가지가 있는데 외부의 변수와 관계없는 에너지의 전달을 열이라 하지요. 온도가 높은 계에서 낮은 계로 열이 이동하면 전체 엔트로피가 증가하게 됩니다. 열역학 둘째 법칙에 의하면 반대로는 일어나지 않는데, 만약 일어날 수 있다면 어떻게 될까요? 열이 차가운 쪽에서 뜨거운 쪽으로 이동할 수 있으니 여름에 컵에 담긴 물이 꽁꽁 얼 수도 있습니다. 이런 일이 생길 수 있다면 냉난방기가 필요하지 않겠지요.
어떤 계를 두 부분으로 나누어서 한쪽을 A, 다른 쪽은 B라고 해보죠. A의 거시상태에 대응하는 미시상태, 곧 접근가능상태의 수를
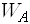
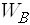
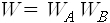
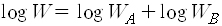
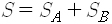
엔트로피는 거시상태를 기술하는데 거시상태는 일반적으로 계의 에너지에 의존하므로 결국 엔트로피는 에너지의 함수입니다. 어떤 계의 에너지가 변화하면 엔트로피도 함께 변화하는데 그 변화량은 엔트로피를 에너지로 미분한 도함수에 에너지의 변화량을 곱하면 됩니다. 식으로는
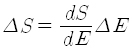
|
로 쓸 수 있지요. 도함수
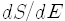
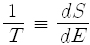
와 같이 나타내지요. [이렇게 정한 온도 T를 절대온도라고 부릅니다. 열 현상에 관해 업적을 남긴 켈빈(Lord Kelvin: 본명은 톰슨William Thomson)의 이름을 따서 만든 켈빈 눈금으로서 K로 표시하지요. 셀시우스(Anders Celsius)의 이름을 딴 셀시우스(한자로는 존칭 '씨'를 붙여서 '섭씨') 눈금과는 273.15 만큼 차이가 납니다. 예컨대 절대영도는 셀시우스 눈금으로 영하 273.15도, 곧 0 K = -273.15 °C 이지요.] 따라서 앞의 식은
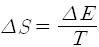
|
로 쓸 수 있습니다.
만일 온도
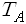
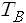
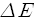
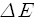
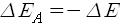
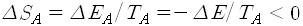
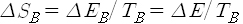
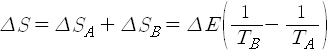

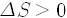
생명이 존재하려면 엔트로피를 끊임없이 줄여주어야 하므로 열역학 둘째법칙에 위배되고, 따라서 전능한 창조주, 하느님이 있어야 한다고 주장하는데 이는 무식한 주장입니다. 둘째법칙은 외떨어진 계에서 성립하는데 생명체는 외떨어진 계가 전혀 아니죠. 바깥세상과 끊임없이 에너지와 물질이 왔다 갔다 하기 때문에 자신의 엔트로피는 낮출 수 있는 겁니다. 말하자면 자신의 엔트로피를 낮추는 대신 주위 환경의 엔트로피를 높이기 때문에 환경을 포함한 전체 계의 엔트로피는 늘어나고, 둘째법칙은 물론 성립하게 됩니다.
이러한 개념이 처음부터 정립되었다면 아마도 온도의 역수 대신에
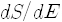
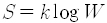
|
로 쓰면 엔트로피의 에너지에 대한 변화율, 곧 도함수가 바로 캘빈 눈금으로 나타낸 온도의 역수가 됩니다.
통계역학을 완성하고 원자라는 개념을 물리학적인 관점에서 확립한 사람이 볼츠만이죠. 볼츠만이 통계역학을 통해 거시적인 관점에서 되짚기 대칭성이 깨진다는 것을 설명했는데 그때는 아무도 믿지 않았어요. 볼츠만이 당시에 펼친 반론은 오늘날 봐도 놀랄 정도로 훌륭합니다. 그러나 당시 사람들은 이에 대해 매우 비판적이었고 결국 볼츠만은 정신병에 걸려 자살했습니다. 정신분열증 같은 병은 아니었고 우울증이었다고 하지요. 물리학사에서 가장 큰 공헌을 한 사람으로 뉴턴을 꼽는다면 그 다음은 글쎄요, 아인슈타인보다는 볼츠만이라고 생각할 수도 있습니다.
오스트리아의 수도인 빈(Wien)에는 볼츠만의 묘소가 있는데 그 묘비에는 바로 위의 엔트로피의 정의식이 쓰여 있어서 유명합니다. 그의 제자로 에렌페스트(Paul Ehrenfest)가 있었는데 이 분도 자살을 했어요. 에렌페스트의 제자로는 울렌벡(George E. Uhlenbeck)이 있었고 울렌벡의 제자로는 조순탁 선생님이 계셨습니다. 우리나라에서 통계역학을 시작하신 분으로 한국과학기술원장을 지내기도 하셨지요. 그 분의 제자로 서울대 교수를 지내신 이구철 선생님이 계시고, 그 분의 제자 중에 최무영이란 사람이 있습니다. 따지고 보면 나는 볼츠만의 5대 손인 셈이죠.
그동안 동역학에서 다뤘던 물리량은 시간, 질량, 길이 등인데 이런 것들에 비해서 온도라는 개념은 성격이 다르다는 느낌이 들지요. 이론과학의 구조에서 길이, 시간, 질량 등은 기본개념들인데 온도는 기본개념이 아니고 엔트로피에 의해서 정의되는 이차적인 개념이기 때문입니다. 엔트로피는 접근가능상태의 수로부터 정의되므로 거시적인 개념이고 이로부터 비로소 정의되는 온도는 상당히 높은 단계에서 이끌어진 파생개념이지요. 그런데 놀랍게도 이러한 온도를 우리 몸은 직접 감지합니다. 우리의 감각기관으로 직접 측정할 수 있다는 말이죠. 기본적인 양은 측정하지 못하면서도 상당히 높은 파생개념의 양을 직접 측정할 수 있다는 것은 놀랍고 생명현상이란 참 특이하다는 사실을 말해줍니다.
학생: 엔트로피라는 개념이 생기기 전에 이미 온도라는 개념을 쓰지 않았나요?
물론이지요. 그런데 엔트로피라는 것을 알기 전에는 온도를 어떻게 정의했을까요? 온도는 인간이 감각으로 직접 측정할 수 있으므로 그 개념은 인류 역사만큼이나 오래 되었다고 할 수 있겠네요. 여러분은 엔트로피를 배우기 전인 초등학교나 중학교 때 온도를 어떻게 배웠나요? 막연히 차고 더운 정도로 배웠겠지요? 엔트로피의 개념 없이는 온도를 정확하게 정의할 수 없고, 대신에 조작적인 정의를 했습니다. 예컨대 보통 물질이 온도가 높아지면 부피가 불어나는 성질을 이용해서 온도를 정하는데 이는 바로 온도계의 원리이지요. 그런데 일반적으로 물질의 부피가 온도에 정확하게 비례해서 불어나지는 않으므로 온도 간격을 등분해서 온도의 눈금을 정하는 것은 사실 엄밀하지 못합니다. 엄밀하게는 이상기체를 통해서 절대온도를 정의할 수 있지만 이상기체란 현실적으로 없고, 또한 이를 통해서 조작적으로 눈금을 정의하더라도 그것이 온도의 본질을 정의하는 것은 아니죠. 그러나 이제는 엔트로피를 아니까 온도의 본질이 무엇인지 정확히 알 수 있습니다.
열이나 엔트로피 등의 용어를 들으면 흔히 열기관(heat engine)을 연상하게 됩니다. 연료를 태워서 연료에 저장되어 있는 화학에너지를 열의 형태로 바꾸고 결국 운동에너지로 바꿔서 쓰는 장치를 열기관이라고 합니다. 여러분이 집에서 학교까지 타고 온 버스 같은 자동차는 모두 열기관을 이용한 거지요. 여기서 연료에 저장되어 있는 에너지 중에 얼마나 운동에너지로 바꾸어 이용하는가를 열효율이라 합니다. 열효율은 높아봤자 30∼40% 정도로서 반에도 미치지 못합니다. 반 이상은 버리는 셈인데, 그냥 버리는 것도 아니고 온갖 오염을 만들죠. 열기관의 효율이 이렇게 낮은 이유는 인간의 기술 수준 뿐 아니라 바로 열역학의 둘째 법칙 때문으로서 본질적인 문제라 할 수 있습니다.
일반상대성이론에 대해서 논의할 때 이미 언급한 에딩턴은 열역학 둘째 법칙이 자연의 모든 법칙 중에 최고, 최상의 위치를 차지한다고 생각했습니다. "만일 누군가 말하기를 우주에 대한 당신의 이론이 맥스웰 방정식과 일치하지 않는다면 맥스웰 방정식이 잘못되었을 수도 있다. 만약 당신의 이론이 관측 결과와 모순된다고 해도 걱정할 필요가 없다. 실험하는 사람들이 틀리기도 하니까. 그러나 당신의 이론이 열역학 둘째 법칙에 위배되는 것으로 밝혀진다면 나는 당신에게 아무런 희망을 줄 수가 없다. 가장 깊은 치욕의 구렁텅이로 빠지는 수밖에 없다." 에딩턴의 저서 ≪물리적 세계의 본성(The Nature of the Physical World)≫에 나오는 말입니다. 뉴턴의 운동법칙이나 슈뢰딩거의 방정식 따위를 기본적인 것으로 생각하는 한편 열역학 둘째 법칙은 절대적인 것이 아니라 가변적이고 부수적인 통계 법칙이라고 생각하기 쉬운데 오히려 반대로 보는 입장이지요.
이러한 엔트로피란 본질적으로 정보의 문제라는 사실은 매우 중요합니다. 다음 강의에서 논의하겠지만 엔트로피는 바로 정보의 부족(missing information)을 나타냅니다. 앞에서 언급했듯이 휠러는 우주의 모든 것이 '알갱이'가 아니고 '마당'도 아니며 바로 '정보'라고 지적했는데, 이러한 정보는 자연을 해석하는 데 핵심적인 도구라 할 수 있습니다.



전체댓글 0