그러면 이러한 계가 처음에 거시상태 1에 있다면 나중에는 어떻게 될까요? 일반적으로 계의 구성원들은 주어진 상태에 그대로 머물러 있지 않고 시간에 따라 계속 상태가 변화합니다. 예컨대 공기 분자는 움직이므로 위치가 계속 바뀌고 충돌을 통해 속도도 끊임없이 바뀌지요. 따라서 계의 상태는 가능한 모든 미시상태를 돌아다니며 그 사이에서 계속 변화하게 됩니다. 그러면 처음에 상태 1에 있었다는 말은 거시상태 1에 대응하는 미시상태 중에 하나에 있었다는 뜻인데 시간이 지나면 다른 미시상태로 옮겨 가겠네요. 그러면 1억 가지 미시상태 중에서 거의 언제나 거시상태 5에 대응하는 미시상태에 있게 될 것입니다. 그 수가 압도적으로 많으니까요. 따라서 처음에 거시상태 1에 있었다하더라도 시간이 지나면 결국 거시상태 5로 돼버릴 것입니다. 그런데 반대로 처음에 거시상태 5에 있었다고 해보지요. 한참 기다리면 언젠가 상태 1로 가겠어요? 일반적으로는 가지 않을 겁니다. 이를 되짚기가 안 된다고 말합니다. 거꾸로 가지 않는다는 뜻으로 한자어로는 '비가역'이라고 하고 우리말로는 '안되짚기'라고 합니다. 시간에 대해서 되짚을 수 없다는 표현이지요.
이 앞에 접두사로 더 좋은 말이 없을까요? 우리 토박이말 중에 무엇이 없음을 나타내기에 적당한 접두사가 있습니다. 여러분은 무척추동물이라고 배웠겠죠. 척추라는 한자어에 해당하는 우리말은 등뼈지요. 등뼈가 없다는 것은 무등뼈라고 하지 않고 민등뼈라고 합니다. 그래서 꽃이 없는 식물은 민꽃식물, 그리고 여름에 소매 없는 옷을 입잖아요. 그것을 민소매라고 하죠. 마찬가지로 머리가 없으면 민머리라고 부릅니다. 정확히는 머리가 없는 것은 아니고 민머리카락이라는 뜻이겠지요. 물리학에서 이음줄(wire)이 없는 것은 민이음줄(wireless)이라 합니다. 이것은 내 멋대로 아무렇게나 쓴 것은 아니고 한국물리학회의 공식 용어로 만들어졌던 것입니다. [사실은 한국물리학회에서 이런 용어를 만드는 작업에 내가 참여했었지요.]
시간되짚기가 없는 현상은 우리 주위에서 흔히 볼 수 있습니다. 예를 들어 향수병을 열면 향기가 퍼져 나가는데, 아무리 기다려도 퍼져 나갔던 향수가 다시 향수병 안으로 들어가는 경우는 없지요. 물에 잉크방울을 떨어뜨리면 잉크가 퍼져서 푸르스름해지는데 그 반대 현상은 일어나지 않습니다. 이같이 되짚기 성질이 없는 현상은 이해하기 어렵고 수수께끼 같은 일입니다. 향기 분자나 잉크 분자 등 구성원 하나하나의 운동은 고전역학에 의해 기술되므로 당연히 시간되짚기 성질이 있습니다. 그런데 구성원 전체를 보면 시간되짚기가 되지 않습니다. 우리가 나이를 먹어서 늙어가기만 하고 다시 젊어지지 못하는 안타까운 현실도 이와 관련되어 있습니다. 우리 몸을 이루는 분자 하나하나는 시간되짚기 성질이 있지만 전체 계로 보면 그렇지 못한 거죠. 말하자면 미시적인 관점에서는 시간되짚기 성질이 있는데 왜 거시적인 관점에서는 그러한 성질이 깨지는가? 이 수수께끼 같은 현상은 통계역학의 중심 문제라고 할 수 있습니다.
엔트로피
여기서 가장 중요하고 핵심적 개념이 바로 엔트로피입니다. 주어진 거시상태에 대응하는 미시상태들은 일반적으로 아주 많은 수가 있는데, 이들을 접근가능상태(accessible state)라고 부르고 그 수를 W로 나타냅니다. 어떤 거시상태냐에 따라서 W값이 다르며, 작을 수도 있지만 보통 거시계에서 엄청나게 크지요.
이러한 접근가능상태의 수는 워낙 크기 때문에 직접 다루기는 매우 불편합니다. 이를 편리하게 다루는 방법이 로그를 택하는 거고 이를 엔트로피라고 합니다. 즉 엔트로피 S는 접근가능상태 수 W의 로그
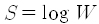
|
로 정의하지요. 당연한 말이지만 엔트로피는 계의 거시상태를 특징짓는 양이므로 거시적 기술에서만 의미가 있습니다.
그러면 거시상태마다 그 상태에 해당하는 엔트로피를 생각할 수 있습니다. 예컨대 거시상태 1에 있는 계의 엔트로피, 거시상태 2에서의 엔트로피 따위로 상태마다 엔트로피가 주어져있는데, 여기서 엔트로피가 크다는 것은 접근가능상태 수가 크다는 뜻이지요. 그 거시상태에 대응하는 미시상태가 많으므로 그 상태에 있을 확률이 더 큽니다. 따라서 엔트로피가 각각 다른 여러 가지의 거시상태가 가능한데 현실적으로는 그 중에서 엔트로피가 가장 큰 거시상태에 있게 됩니다.
잉크방울을 물에 떨어뜨리는 경우 잉크방울과 물이 따로따로 있는 것은 엔트로피가 작은 상태이고 잉크가 퍼져 물과 섞여서 푸르스름해지는 상태가 엔트로피가 가장 큽니다. 주어진 계가 엔트로피가 작은 상태에서 큰 상태로는 변화하지만 그 반대는 일어나지 않습니다. 자주 들어봤겠지만 이것이 바로 열역학의 둘째 법칙입니다. 정확히 표현하면 "외떨어진 계의 상태는 계의 엔트로피가 감소하는 방향으로는 바뀔 수 없다"고 하지요.
여기서 상태는 물론 거시상태를 뜻하고, 엔트로피가 저절로 줄어들 수는 없다는 것이 둘째 법칙의 핵심입니다. 처음에 이미 엔트로피가 큰 상태였다면 계속 그 상태로 있을 수도 있지요. 따라서 엔트로피의 변화량, 곧 나중 상태의 엔트로피와 처음 상태의 엔트로피의 차이를
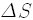
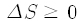
|
으로 표현할 수 있습니다.



전체댓글 0