여기서 혼돈이라고 부르는 이유는 무엇일까요? 주기적으로 거동하지는 않지만 결정론적이므로 처음 값이 주어지면 나중 값이 완벽히 결정돼 있습니다. 그런데도 혼돈이라 부르는 이유는 초기조건에 아주 민감하기 때문입니다. 주사위와 마찬가지이지요. 주사위의 운동도 고전역학으로 기술되니까 결정론적입니다. 주사위를 어떤 높이에서 어떤 속도를 줘서 던질지 정하면 주사위의 운동은 완벽하게 결정됩니다. 바닥에 떨어져서 뭐가 나올지는 사실 결정돼 있는 거지요. 그렇지만 현실적으로 무엇이 나올지 예측할 수는 없습니다. 처음에 던져서 6이 나왔는데 아무리 똑같은 초기조건을 주고 던져도 다시 6이 나오지는 않지요. 왜냐하면 초기조건을 아무리 똑같이 주더라도 조금은 틀릴 수밖에 없기 때문입니다. 똑같은 모양으로 잡더라도 각도가 조금은 틀릴 것이고, 속도를 똑같이 준다 하더라도 조금은 틀리게 줄 수밖에 없죠. 초기조건을 아무리 정확히 맞추더라도 약간의 오차가 있기 마련인데, 초기조건이 조금만 틀리면 결과는 완전히 달라집니다. 그래서 6이 될 수도 있고 2나 3이 될 수도 있는 거죠. 이러한 현상을 두고 "초기조건에 민감하다"고 말합니다. 이 때문에 형식적으로는 결정론이라 하더라도 실질적으로는 예측을 할 수 없어요, 초기조건이 조금만 달라도 결과는 완전히 다르니까. 이를 나비효과라 부른다고 앞에서 말했지요.
일기예보에서도 바람이 어떻게 불고, 대기의 습도가 어떻게 변하고, 온도가 어떻고, 이런 걸 예측하는데 이들은 모두 고전역학으로 기술됩니다. 따라서 본질은 결정론적입니다. 그러나 초기조건을 완벽하게 제어할 수는 없는데 초기조건에 조금만 오차가 있어도 결과는 완전히 달라질 수 있습니다. 예를 들어 초기조건이 1.001이라면 맑은 날씨인데, 1.002이면 갑자기 눈이 오는 날씨가 되는 거지요. 초기조건이 조금만 달라도 결과가 완전히 달라지는 이러한 현상이 바로 혼돈입니다. 원리적으로는, 곧 기술하는 동역학 자체는 결정론이지만 초기조건에 워낙 민감하기 때문에 실제로는 예측할 수가 없는 거지요.
|
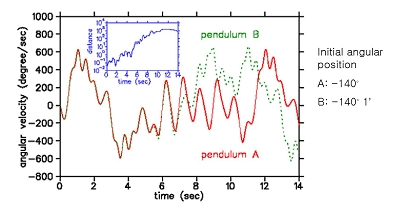
비슷한 예로서 그네 또는 흔들이를 밀어주는 경우를 들 수 있습니다. 마구잡이로 미는 게 아니라 규칙적으로 밀어주는 거지요. 흔들이의 길이가 1 m 인데 이를 진동수 1 Hz로, 곧 1초에 한 번씩 주기적으로 밀어줍니다. 그런데 이렇게 몰리는 흔들이(driven pendulum)의 각속도가 시간에 대해 어떻게 변하는지를 그래프로 나타낸 그림 7에서 보다시피 흔들이의 거동은 무질서하고 마구잡이로 변하는 듯합니다. 그러나 사실은 흔들이의 시간변화를 기술해주는 방정식도 마찬가지로 뉴턴의 운동방정식이므로 모든 것이 결정론적으로 변하는 거지요. 그런데 흔들이는 왜 마구잡이로 거동하는 듯이 보일까요?
흔들이가 처음 각위치가 140˚에서 시작했다고 합시다. 그러면 그 거동은 그림 7에서 빨간 선으로 주어집니다. 다음에는 처음 각위치를 140˚ 1'로 주고 시작했습니다. 그러니까 초기조건을 불과 각도 1분, 곧 1/60도만큼만 바꾸고, 나머지는 똑같이 한 거예요. 이 경우 거동을 초록빛 점선으로 표시했는데 처음에는 빨간 선과 비슷하게 가다가 놀랍게도 7초 쯤 지나면서부터 달라지더니 곧 완전히 달라집니다. 그러니 초기조건을 조금만 바꿨는데도 결과는 완전히 다르게 되네요. 이런 것이 바로 혼돈이지요.
이렇게 초기조건이 조금만 달라도 결과가 완전히 달라지는 상황에서는 예측할 수 없습니다. 이른바 예측불가능(unpredictability)이지요. 여기서 강조할 점이 있습니다. 예측불가능이란 인간이 좀 모자라기 때문일까요? 인간의 능력이 더 뛰어나서 초기조건을 정확하게 줄 수 있으면 예측할 수 있지 않을까요? 그렇지 않습니다. 초기조건을 아무리 정확히 주더라도 무한히 정밀하게, 곧 완벽하게 줄 수는 없습니다. 셈틀로 계산한다 해도 셈틀이 무한한 자릿수를 다 계산할 순 없어요. 아무리 기억용량이 큰 셈틀이라 해도 소수점 이하 열 몇 자리, 이런 정도겠지요. 사실 유한한 세계에서 무한히 많은 정보를 처리할 수는 없습니다. 우리 우주에서 원리적으로 불가능하지요. 그래서 예컨대 소수점 이하 스무 자리까지 계산했다고 하면 스물 한 자리에는 오차가 있기 마련입니다. 그러면 그 소수점 이하 스물 한 자리에 있는 오차가 시간이 조금 지나면 놀랍게도 완전히 다른 결과를 가져오게 됩니다.
이는 본질적으로 실수(real number)의 성질과 연관되어 있습니다. 일상에서 보통 생각하고 사용하는 수를 말하지요. 그러니까 혼돈과 관련해서 예측불가능이란 인간 능력의 문제가 아니라 자연을 기술하는 실수 자체의 성질 때문에 생겨납니다. 놀랍지요.
유명한 예로 빵반죽 변환(baker's transformation)이라는 것이 있습니다. 이건 이차원 (x,y)평면에서 정의되는데,
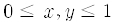
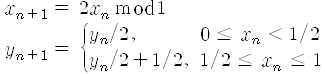
|
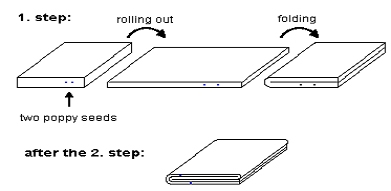
대체로 x방향으로 두 배 늘리고y 방향으로는 반으로 줄이는 것을 되풀이하라는 얘기지요. 이것을 그림으로 나타내면 훨씬 이해하기 쉽습니다. 그림 8에서처럼 먼저 직육면체의 빵 반죽을 눌러서 두께를 반으로 줄입니다. 그러면 길이가 두 배로 되겠죠. 다음에 이걸 반으로 접습니다. 접은 다음엔 원래 모양으로 되돌아갔죠? 이걸 계속 되풀이하는 것이 빵반죽 변환입니다. 사실 원래 빵반죽 변환은 반죽을 접는 게 아니라 잘라서 위에다 붙이는 거지만 사실상 마찬가지죠. 혹시 수타 짜장면 반죽하는 거 봤어요? 바로 이렇게 하지요.
|
반죽에 건포도가 있었다면 이 변환을 반복함에 따라 서로 모여 있던 건포도가 멀리 떨어지게 됩니다. 반죽을 할 때 이런 과정을 몇 번 되풀이하면 아주 골고루 섞이게 되지요. 말하자면 두 개의 건포도의 처음 위치가 조금만 달라도 변환을 몇 번 하면 완전히 다른 위치로 가게 됩니다. 이게 바로 "초기조건에 민감하다"는 뜻이지요. 그러니 반죽에서 밀가루와 설탕이나 건포도를 고르게 섞으려고 굳이 애를 쓸 필요가 없어요. 빵반죽 변환만 몇 차례 되풀이하면 매우 고르게 섞이게 됩니다.
|
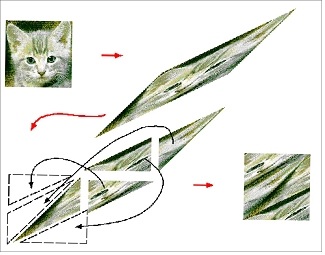
비슷한 예로 고양이 본뜨기(cat map)라는 것도 있습니다. 역시 바른네모꼴의 고양이 얼굴을 대각선 방향으로 누릅니다. 고양이 얼굴이 찌그러지죠. 그 다음에 이것을 그림 9처럼 잘라서 갖다 붙이면 원래 바른네모로 되돌아옵니다. 그러면 불쌍한 고양이가 이렇게 엉망이 됐는데 아직 고양이 같은 모양이 좀 남아있지만 이를 서너 번만 되풀이하면 완전히 섞여서 고양이는 오간데 없어집니다. 고양이한테 너무 못할 짓 했나요? 아무튼 이것은 본질적으로 빵반죽 변환하고 똑같습니다.
이런 것이 바로 초기조건에 민감하다는 현상의 예이고 따라서 예측불가능을 의미합니다. 수학적으로는 동전던지기, 곧 동전을 던져서 앞면 또는 뒷면이 나오는 현상과 사실상 동등하지요. 그런데 보듯이 이러한 변환은 매우 간단한 식으로 기술됩니다. 마찬가지로 앞에서 예로 든 몰리는 흔들이도 간단한 운동방정식으로 기술되는데 불구하고 혼돈 현상을 보이지요. 한편 일식이나 살별(혜성)을 비롯한 천체의 운동은 완벽하게 예측합니다. 앞서 지적했듯이 언제 살별이 돌아오고 일식이 일어나는지 몇 백 년 후를 정확히 예측하면서 날씨는 불과 이틀 후를 예측하지 못합니다. 몰리는 흔들이는 몇 분 후도 예측하지 못하지요. 다시 강조하지만 이들은 모두 똑같이 고전역학에 의해 기술되고 있습니다. 그럼에도 불구하고 이렇게 상황이 완전히 다르지요.



전체댓글 0