역학에서 상태의 변화 또는 운동은 보통 수학적으로 미분방정식 형태로 기술합니다. 여러 번 지적했지만 고전역학의 운동방정식 a=F/m에서 가속도 a는 위치를 시간에 대해 두 번 미분한 2차 도함수입니다. 따라서 이 식에서 구한 가속도를 적분하면 속도와 위치를 구할 수 있습니다. 초기조건, 곧 처음의 위치와 속도가 정해지면 이 방정식으로부터 나중 상태, 곧 임의의 순간에서 위치와 속도가 얻어지지요.
일상경험에서 시간은 연속적으로 흐릅니다. 미분이란 아주 짧은 시간 동안에 변화를 나타내는 수학적 형식이지요. 그런데 간단하게 하기 위해서 시간이 띄엄띄엄하다고 생각해볼까요. 하긴 극히 짧은 시간에 대해서는 잘 모르니까 어쩌면 시간이 마치 전기량처럼 기본양이 있을지도 모르지요. 아무튼





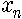
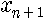
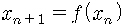
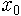
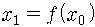
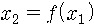
예를 들어 보지요. 어느 외딴 섬에 벌레가 사는데 가을마다 b개의 알을 낳고 죽는다고 합시다. 봄이 오면 알이 까서 벌레가 되지요. 그럼 n년째의 벌레의 수를
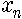
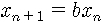
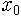
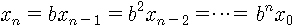
여기서 b는 당연히 1보다는 크겠죠. 그럼 n이 커지면
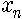
그런데 실제로는 이렇지 않을 것입니다. 왜 그렇죠? 우선 섬 안에 먹이가 한정되어 있을 테니까 벌레가 너무 많아지면 먹이가 모자라서 못 살 겁니다. 설령 먹이가 풍부하더라도 좁은 곳에 너무 많이 가두면 끼리끼리 싸워서 서로 죽이고 난리가 나잖아요. 벌레도 그렇고 쥐들도 그렇고 당연히 사람도 그렇지요. 서로 싸우고 먹이도 부족하게 될 테니까 결국 벌레가 무한히 증가하는 게 아니라 어떤 수를 넘어서지는 못하게 됩니다. 섬에서 살 수 있는 벌레 수의 최대값
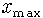
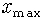
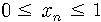
아무튼 벌레가 너무 많으면 오히려 삶의 질이 저하되니까 벌레 수에 단순히 알의 수 b만 곱한 것이 아니라 서로 억제하는 효과를 나타내는 요소
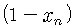
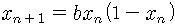
|
을 얻는데 이를 병참본뜨기(logistic map)라고 부릅니다. 널리 알려진 식이지요.
이 식에서 n이 0에서 1, 2, 3, …… 으로 계속 늘어나면서
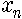
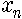
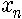
일반적으로 b가 작아서 0과 3 사이의 값을 가지면 계는 안정되어 있습니다. 다시 말해서 알을 조금씩만 낳으면 벌레 수는 하나의 값으로 주어지게 된다는 거지요. 그 값은 해마다 똑같고 변하지 않으므로 붙박이점(fixed point)이라고 부릅니다. 이는 병참본뜨기에서
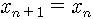
|
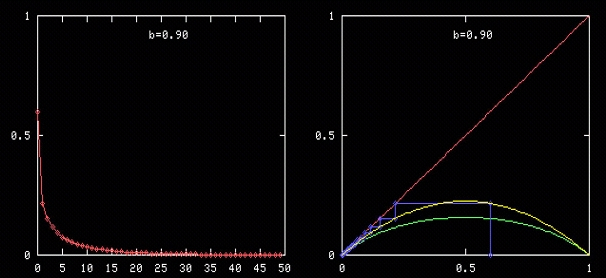
특히 b가 0과 1 사이면 그림 1에 보였듯이 포물선과 직선이 만나는 점은 원점밖에 없습니다. 이게 무슨 얘기죠? 처음 벌레 수
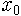
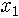
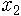
사람 사회로 얘기하면, 인구가 계속 감소해서 멸종한다는 겁니다. 벌레와 달리 사람은 남자와 여자가 만나서 애를 만들므로 b의 경계값은 1이 아니라 2가 되겠지요. 그러니 부부가 결혼을 해서 애를 둘보다 적게 낳으면 인구가 계속 줄어든다는 얘깁니다. 지극히 당연하지요. 시간이 한참 지나면 결국 0으로 끌려가게 되므로 이 때 끌개는 0이라는 붙박이점이네요.
그런데 b가 조금 더 커져서 1을 넘어서면 재밌는 현상이 생깁니다. 다음 그림 2에서처럼 b가 1보다 크고 3보다 작으면, 직선과 포물선의 사귐점이 0 말고 하나 더 있습니다. 그림 2와 같이 b=2.8인 경우 처음에
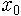
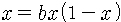
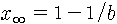
|
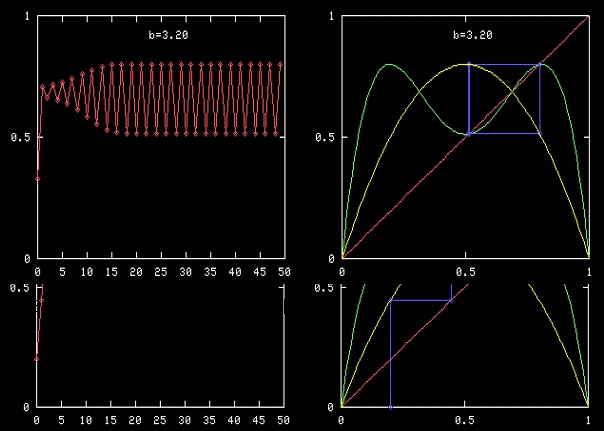
그런데 b가 3보다 커지게 되면 놀랍게도 주기적인 진동을 보입니다. 벌레 수가 해마다 일정하지 않고 변한다는 얘기지요. 그림 3에서 보였듯이 처음 값에서 출발해서 어떤 한 값에 수렴하는 것이 아니라 두 값에서 계속 왔다 갔다 합니다. 이렇게 해서 한 해는 벌레 수가 많고 한 해는 벌레 수가 적고, 많았다 적었다 많았다 적었다 해마다 변하는 거예요. 주기가 2년이 되는 거죠. 붙박이점이 아니라 이렇게 왔다 갔다 주기적으로 변하는 상태의 끌개가 끝돌이입니다.
|
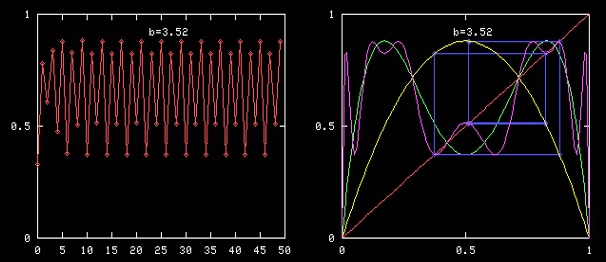
여기서 b가 더 커지면 아주 흥미로운 현상이 생겨납니다. b가 조금 더 커져서 3.52가 되면 그림 4에서처럼 4년을 주기로 변하게 됩니다. 이 그림은 조금 복잡한데 이렇게 네 번 왔다 갔다 해서 원래 값으로 돌아가게 돼 있어요. 벌레 수가 아주 많았다가 아주 적었다가 조금 많았다가 조금 적었다가 다시 아주 많았다가 아주 적었다가 이렇게 해서 4년을 주기적으로 바뀝니다. b가 3.52보다 조금 더 커지면 주기가 이제는 8년이 되지요. 더 커지면 주기가 16년이 되고, 이런 식으로 주기가 계속 두 배로 늘어납니다. 처음에
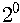
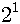
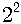
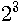
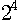
|
이같이 주기가 두 배로 되면서 상태도 두 배로 늘어나는 현상을 주기 겹되기 쌍갈래질(period doubling bifurcation)이라고 부릅니다. 쌍갈래질이란 어떤 방정식의 풀이가 하나에서 둘로 나눠지는 걸 말합니다.
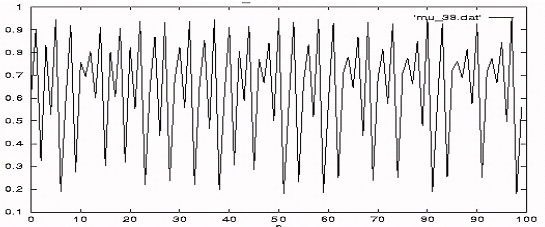
그러면 b값이 정말 커지면 어떻게 되느냐, 예를 들어서b = 3.8 일 때는 그림 5에서 벌레 수의 변화가 해마다 마구 달라져 왔다 갔다 하는데 도대체 주기적이 아닌 것으로 보입니다. 확실하게 하기 위해서 이를 확대해서 어느 한 부분을 자세히 살펴보아도 주기적이지 않음을 알 수 있습니다. 원래 값으로 정확히 돌아오지 않지요. 그러니까 주기적이지 않고 결국 마구잡이처럼 변하는 겁니다.
이것이 바로 혼돈이라고 부르는 현상입니다. 흥미로운 점은 이를 지배하는 식이 매우 간단한 2차식이라는 사실이지요. 정말로 간단한 식이라 처음 값
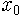
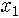
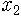
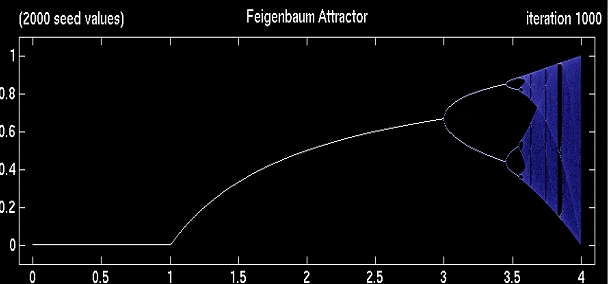
다음 그림 6은 쌍갈래질 그림으로, 가로축의 값에 따라 끌개가 어떻게 되는지 보여줍니다. 먼저 0 < b < 1이면 끌개가 붙박이점 0이라고 그랬죠. 벌레든 인류든 다 멸종한다고 했어요. b > 1이 되면 끌개는 마찬가지로 붙박이점이긴 하지만 0이 아니게 됩니다. b가 커져서 3이 되면
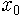
|



전체댓글 0