학생: 양자역학이 현대기술에 어떻게 이용되나요?
양자역학 자체를 직접 이용한다기보다 양자역학이 그런 기술의 바탕이 되었다고 할 수 있습니다. 셈틀(컴퓨터)을 포함한 모든 전자기술에서 가장 중요한 요소가 반도체입니다. 반도체가 없으면 전자기술이란 성립할 수가 없어요. 예컨대 셈틀의 핵심 부품들은 모두 반도체로 만든 거지요. 그런데 반도체가 어떻게 존재할 수 있느냐를 설명하는 것이 양자역학입니다. 양자역학이 없으면 반도체를 전혀 이해할 수 없지요. 반도체란 고전역학으로는 다룰 수 없고 양자역학 때문에 알게 된 것입니다.
요새 휴대용 셈틀(laptop computer), 이른바 공책(notebook)이라 부르는 셈틀의 마구기억장치(RAM; random-access memory)의 용량은 얼마나 되죠? 보통 1 기가바이트(GB), 곧 10억 바이트 정도인가요? [바이트(byte)란 정보의 단위라 할 수 있는데 뒤에 다루려 합니다.] 내가 학생이었을 때 대학 행정관 - 본부라는 이상한 이름으로 불렀지요 - 건물 3층이 전산실이었는데 셈틀이 한 대 있었고 이것이 사실상 3층 전체를 차지했습니다. 아이비엠(IBM) 360이라는 셈틀이었는데 기억장치가 256MB(메가바이트)이었던 것으로 기억합니다. 농담으로 들리지요? 먼 옛날이 아니라 30여 년 전만 해도 그랬습니다. 그것이 불과 30여 년 사이에 엄청나게 달라진 것입니다. 하기는 요새 우리나라는 다시 뒷걸음쳐서 2MB의 시대라고도 하더군요.
이같이 달라진 것은 자꾸 크기를 줄일 수 있었기 때문입니다. 여러분 진공관(vacuum tube)이란 것 본 적 있어요? 들어본 적도 없죠? 트랜지스터(transistor)는 들어봤어요? 요새는 트랜지스터도 쓰지 않죠. 내가 어렸을 때는 진공관이 많이 쓰였는데 그 크기가 어린이 손만했지요. 그것이 나중에 트랜지스터로 바뀌면서 손톱만해졌고, 다시 집적회로(IC; integrated circuit) 소자로 되면서 모래알 정도 크기가 됐어요. 이런 식으로 소형화가 가능했기 때문에 개인용 컴퓨터를 만들 수 있었던 것입니다.
트랜지스터란 결국 전기신호를 제어하고 조절해서 여러 가지 원하는 작동을 할 수 있도록 합니다. 이에 필요한 전기량을 점점 작게 해서 결국에는 전자 하나로 제어하는 것이 기술자들의 꿈입니다. 그것을 홑전자 트랜지스터s(ingle-electron transistor)라고 불러요. 우리가 생각할 수 있는 최소량이 전자 하나잖아요? 전기량으로 따지면
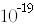
그러니까 셈틀이나 휴대전화를 작게 만들려면 - 사실 휴대전화는 사람들 손에 쥐어져야 하니까 너무 작게 만들 수는 없겠죠 - 소자 자체를 점점 작게 만들어야 합니다. 그러려면 궁극적으로 전자 하나를 제어할 수 있어야 하고, 여기에 양자역학이 본질적인 한계를 주게 됩니다. 양자역학을 이해하지 못하면 이런 것을 생각도 할 수 없어요.
그리고 생물기술도 마찬가지죠. 유전공학 자체가 분자생물학에서 출발한 것입니다. 분자생물학이란 생명현상을 분자 수준에서 고찰해보자는 것이고 이러한 분자 수준에서의 고찰은 본질적으로 양자역학의 이해가 필요한 것이죠.
다른 질문 없어요?
학생: 파동함수라고 말씀하셨던 것이 전자의 상태를 나타내는 것인데 상태를 확정할 수 없는 것이 불확정성 원리라고 말씀 하셨잖아요? 그러면 전자의 상태를 알 수 없다는 말 아닌가요?
불확정성원리란 상태를 무조건 확정할 수 없다는 뜻이 아니라 우리가 재는 물리량들 중에서 어떤 것들끼리는 서로 양립할 수 없다는 뜻입니다. 물리량들은 여러 가지가 있습니다. 질량, 전기량, 속도, 에너지 등 매우 많지요. 스핀도 그 중 하나인데, 고전역학에서는 이런 양들을 얼마든지 정확하게 잴 수 있습니다. 측정 기술이 모자라서 문제이지, 적어도 원리적으로는 원하는 대로 정확하게 잴 수 있지요.
그런데 양자역학에 의하면 그런 여러 가지 양들 중에서 서로 양립할 수 없는 것들이 있습니다. 대표적인 것이 같은 방향의 위치와 속도 (또는 운동량) 성분이지요. 그중에 하나는 정확히 잴 수 있지만 둘을 같이 정확히 잴 수는 없다는 말입니다. 어느 하나를 재면 남은 하나는 정확히 잴 수 없는데, 이것이 불확정성원리입니다. 그래서 위치 성분 x와 같은 방향의 운동량 성분
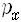
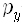
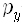
이는 앞에서 논의한 스핀과 마찬가지입니다. 스핀의 z성분을 재면 그것의 고유상태로 환원되지요. 그런데 x성분을 다시 재면 x성분의 고유상태로 바뀌게 되므로 z성분의 고유상태는 깨지게 됩니다. 스핀의 x성분의 고유상태면서 동시에 z성분의 고유상태라는 것은 없습니다. 그 두 가지가 서로 양립할 수 없는 물리량이기 때문이지요. 마찬가지로 우리가 위치를 재면 위치의 고유상태로 환원되지만 다시 속도를 잰다면 이제는 속도의 고유상태가 되지요. 그런데 속도의 고유상태는 위치의 고유상태가 될 수 없습니다. 둘은 서로 양립하지 않아요. 따라서 더 이상 위치를 알 수 없게 되는 것입니다.
학생: 위치를 정확하게 잰다는 것은 측정이라고 말할 수 있는 것인가요?
글쎄요, 질문의 정확한 뜻을 잘 모르겠는데, 아무튼 측정이란 잰다는 얘기지요. 위치를 정확히 재는 것은 물론 위치를 정확히 '측정'하는 것입니다. 그러면 대상의 상태함수가 위치의 고유함수로 환원되지요. 어떤 알갱이의 위치를 재서 여기 있다는 결과를 얻었습니다. 그러면 그 알갱이는 이 위치에 있는 고유상태에 있게 된 것입니다. 여기서 다시 위치를 재면 그 고유상태 그대로 있지요. 위치는 정확히 정해져 있는 것입니다.
그런데 여기서 속도를 재면 알갱이의 상태는 속도의 고유상태로 바뀌게 됩니다. 그러면 알갱이는 더 이상 위치의 고유상태에 있지 않습니다. 다시 말해서 속도의 고유상태에 있으니까 속도는 정확히 말할 수 있지만 위치가 어디인지는 말할 수 없다는 거지요.
학생: 위치가 정확하게 정해진다는 것은
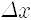
그렇죠. 정확하게 잰다면.
학생: 속도라고 하면
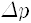
일단 위치를 재서 위치의 고유상태로 되면 속도는 전혀 알 수 없습니다. 조금 전문적인 얘기지만 위치의 고유상태는 엄청나게 많은 수의 속도의 고유상태들이 포개져 있는 상태입니다. 가능한 속도의 고유상태들이 매우 많은데 그런 것들이 포개져 있으니까 그들이 어떻게 될지 속도를 재기 전에는 말할 수 없는 것이죠. 물론 속도를 재면 그 중에 어느 한 값이 얻어져서 속도가 결정되겠지만, 그러면 더 이상 위치의 고유상태가 아닙니다. 거꾸로 속도의 고유상태로서 엄청나게 많은 수의 위치의 고유상태들이 포개져 있는 상태로 되지요. 따라서 위치가 어디인지 말할 수 없는 것입니다.
학생: 파동함수를 측정한다는 것은 정확하게 어떤 의미인가요?
좋은 질문이지만, 내가 언제 파동함수를 측정한다고 했어요? 일반적으로 파동함수는 물리량이 아닙니다. 따라서 측정하는 양이 아닙니다. 그런데 파동함수에 물리적 실재성(physical reality)을 생각할 수 있느냐는 매우 흥미로운 문제입니다. 가능하다, 곧 파동함수의 실재성을 인정할 수 있다는 주장이 제기되었지만 이는 논란이 있습니다.
마지막으로 시간되짚기에 대해 생각해보지요. 고전역학에는 시간되짚기 대칭성이 있다고 말했습니다. 말하자면 공을 던져서 날아가는 광경을 동영상으로 찍은 다음에 거꾸로 돌려도 이상하지 않다는 것입니다. 이는 뉴턴의 운동방정식에서 시간에 음(-)부호를 붙여서 되짚어도 식은 똑같기 때문입니다. 따라서 고전역학은 시간되짚기 대칭성을 지니고 있고, 결국 과거와 미래의 구분이 없다고 지적하였지요.
그러면 양자역학에서는 어떨까요? 양자역학에서 시간변화(time evolution)을 기술하는 식이 슈뢰딩거방정식이지요. 이는 뉴턴의 운동방정식과 달리 시간에 대해 한번만 미분한 꼴이므로 시간에 (-)부호를 붙이면 전체의 부호가 바뀌게 됩니다. 따라서 시간되짚기 대칭이 없는 것처럼 보이지만 사실은 그렇지 않습니다. 왜냐하면 양자역학에서 상태함수는 절대값을 제곱해야 물리적 의미를 지니고 물리량을 주기 때문에 상태함수와 그것의 복소켤레는 같은 것을 나타냅니다. 복소켤레를 택하면 결국 (-)부호가 없어지므로 원래 방정식과 같아지지요. 따라서 슈뢰딩거 방정식도 시간되짚기 대칭을 지녔습니다.
그런데 문제는 측정입니다. 측정에 대해서는 시간되짚기 대칭이 없는 듯 보이지요. 측정하면 계의 상태함수가 갑자기 고유함수로 바뀝니다. 그 반대로는 가지 않아요. 측정이 없으면 전자나 양성자, 원자, 분자 같은 대상계가 양자역학에 따라 시간변화하는 현상을 찍어서 동영상을 만들고 거꾸로 돌려도 이상하지 않습니다. 그러나 그 사이에 누군가 측정을 하고 그것까지 포함해서 동영상을 만들어 거꾸로 돌린다면 금방 알아차릴 수 있을 것입니다.
사실 측정에서 시간되짚기 대칭의 존재 여부는 쉬운 문제가 아닙니다. 측정 과정 자체를 기술하는 방정식은 과연 무엇인가 의문을 가질 수도 있고, 양자역학 해석에서 논란이 있는 문제지요. 나중에 기회가 되면 다루겠습니다.
실제로 양자역학을 응용하는 사람 입장에서 보면 이런 해석의 문제는 중요하지 않습니다. 머리가 복잡해지니까 아무런 생각이 없이 그냥 슈뢰딩거방정식이라는 편미분방정식을 풀어서 파동함수를 구해내는 것에만 관심이 있습니다. 사실 양자역학 자체가 현실적으로는 문제풀이 기술(problem-solving technique) 역할만 하고 있습니다.
예를 들어 반도체를 설계하려면 실리콘이나 갈륨 따위로 적절한 구조를 만드는데 거기서 전자들이 어떤 상태에 있게 되는지 알아야 합니다. 슈뢰딩거방정식을 풀어서 전자의 상태함수를 구하지요. 그러면 이것이 이렇게 되는구나하고 이제 어떻게 해야지 되겠구나 하고 나아가는 것입니다.
기술자들과 마찬가지로 대부분 물리학자들도 양자역학이 자연의 이해와 관련해서 우리에게 주는 진정한 의미가 무엇인가는 잘 생각하지 않는 편입니다. 여러분이 양자역학의 구조와 해석, 개념과 본질적 문제 등에 대해 깊이 있는 성찰을 한다면 물리학을 전공한 학생들보다 양자역학을 오히려 잘 이해한다고 할 수도 있지 않을까요.
(매주 화, 목, 금 연재)



전체댓글 0