고전역학에서는 대상의 상태를 위치와 속도로 규정했는데, 위치와 속도는 개념도 명확하고 실제로 측정하는 물리량에 해당합니다. 그러나 양자역학에서 상태는 이른바 상태함수라는 것으로 규정하는데, 이는 우리가 측정하는 물리량과 직접 관련이 없어요. 따라서 고전역학에서 상태는 우리가 직접 관측해서 재는 물리량에 해당하지만 양자역학에서는 그렇지가 않으므로 우리가 실제로 물리량을 잴 때 그것이 상태함수와 어떤 관련이 있는지 맺어주어야 합니다. 상태로부터 물리량을 얻어내는 규칙이 따로 있어야 하지요. 그래서 양자역학에서는 고전역학에서와 달리 상태, 곧 이론체계와 물리량, 곧 감각기관을 통한 실제세계를 연결하는 해석(interpretation)이라는 문제가 제기됩니다.
측정과 고유상태
양자역학의 관점에서는 대상계의 상태가 상태함수로 기술되는데 상태함수를 구하는 방법으로 슈뢰딩거의 형식이 가장 잘 알려져 있습니다. 곧 슈뢰딩거방정식을 풀어서 상태함수를 구할 수 있고, 이러한 상태함수는 그 대상이 가질 수 있는 여러 가지 가능한 상태들을 기술합니다. 일반적으로 계의 상태는 가능한 상태들, 이른바 고유상태들이 포개져 있는 결합으로 표현됩니다.
그런데 우리가 그 계에서 어떤 물리량을 측정하면, 예컨대 위치를 재거나 속도를 재거나 하면 어떤 특정한 값, 이른바 고유값(eigenvalue)을 얻게 됩니다. 이 때 계는 가능한 고유상태 중에서 측정된 고유값에 해당하는 하나의 특정한 상태로 바뀌어 있게 됩니다. 여러 가지 가능한 고유상태들이 포개져 있었는데 측정을 하면 그 중 하나의 고유상태로 갑자기 바뀌게 되는 거지요. 이를 상태(함수)의 환원 또는 붕괴라고 부른다고 했습니다.
이 중에서 어떤 고유상태로 바뀌느냐는 명확히 말할 수는 없고, 다만 각 고유상태로 바뀔 확률만 얘기할 수 있습니다. 일반적으로 계가
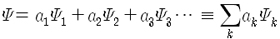
|
와 같이 곁수
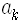
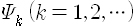
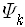
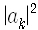
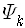
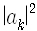
그래서 측정을 하면 계는 어떤 고유상태로 환원되면서 특정한 고유값을 얻겠지만 측정하기 전에는 계가 일반적으로 여러 고유상태들이 포개져 있는 상태에 있으므로 측정해서 어떤 값을 얻을지는 알 수 없고 다만 확률로만 말할 수 있는 것입니다. 이것이 양자역학의 기본 전제입니다.
혹시 질문 없어요? 모두 잘 알아서 질문이 없나요, 아니면 전혀 몰라서 질문이 없나요? 글쎄, 모두 잘 알기는 어려울 것 같은데...
학생: 고유상태의 종류는 어떻게 알 수 있죠?
물론 상황에 따라 결정되는데 일반적으로 대상계를 기술하는 해밀토니안이 주어지면 가질 수 있는 고유상태들이 정해집니다. 언젠가 에너지가 보존된다는 사실은 시간진행에 대해 대칭성이 있음을 뜻한다고 했는데 기억하나요? 이 점에서 에너지는 다른 물리량, 예를 들어 위치나 운동량보다 특별하다고 할 수 있습니다. 물리량들의 값이 시간에 따라 변하지 않는 상태를 정상상태(stationary state)라 하는데 이는 바로 에너지의 고유상태로 주어집니다. 다시 말해서 에너지를 나타내는 해밀토니안의 고유상태에 해당하지요. 물론 다른 물리량에 해당하는 고유상태들도 생각할 수 있습니다. 사실 계의 상태는 임의의 물리량의 고유상태들, 예컨대 에너지의 고유상태들이나 또는 운동량의 고유상태들의 포개진 형태로 나타낼 수 있습니다. 실제로 측정하려는 물리량의 고유상태들로 나타내는 것이 편리하므로 앞에서 그렇게 전제하고 논의하였습니다.
측정과 관련해서 양자역학의 특이한 면을 소개하지요. 스핀의 예를 들어서 설명하겠습니다. 앞서 얘기했지만 전자나 양성자 같은 기본입자는 질량과 전기량 등과 더불어 스핀이라고 부르는 성질도 갖고 있습니다. 이러한 기본입자들로 이루어진 원자도 마찬가지지요.
비유적으로 말하면 스핀이란 전자나 양성자 등이 스스로 도는데, 곧 자전하는데 얼마나 빠르게 하느냐 하는 성질입니다. [이것은 비유일 뿐이고 실제로 자전하고 있는 것은 아닙니다.] 그러면 공간 좌표축을 생각해서 x축이나 y축, 또는 z축을 중심으로 하는 세 가지 방향으로 도는 것이 가능합니다. 따라서 스핀이라고 하는 물리량을 잴 때 세 축 방향으로 각각 잴 수 있으며, 이를 각각 스핀의 성분이라고 부릅니다. 사실 스핀이란 물리적으로 보면 바로 각운동량(angular momentum)이라는 양입니다. 이는 위치나 속도처럼 벡터이므로 x, y, z 방향으로 세 성분을 가지지요.
그런데 예를 들어 전자나 양성자의 스핀의 어느 한 성분, 예컨대 z성분을 잰다면 그 측정값이 +1/2이나 -1/2의 두 가지만 가능합니다. [여기서 단위는 플랑크상수 h입니다. 즉 스핀의 측정값은 ±h/2 이지요.] 다시 말하면 스핀의 고유값이 각각 +1/2과 -1/2인 두 가지의 고유상태를 가질 수 있는 것입니다. 그래서 전자나 양성자는 스핀 1/2을 가졌다고 말하지요.
그러면 양성자들의 스핀의 성분을 재서 그 값이 -1/2인 것들은 버리고 +1/2인 것들만 골라낸다고 합시다. 스핀 값이 두 가지로 다른 양성자들을 구분하려면 방향으로 균일하지 않은 자기마당을 걸어주면 됩니다. 이러한 자기마당에서 양성자는 스핀의 값의 부호에 따라 서로 반대 방향으로 힘을 받기 때문에 +1/2인 것과 -1/2인 것을 구분할 수 있습니다.
여기서 골라낸 양성자들의 스핀을 다시 잰다고 합시다. 스핀의 z성분을 또 재면 어떤 값이 얻어질까요? 당연히 +1/2이 될 것입니다. 그런데 만일 z성분 대신에 x성분을 재면 어떨까요? 골라낸 양성자들은 스핀의 z성분이 +1/2이지만 성분은 +1/2인 것들과 -1/2인 것들이 같이 섞여 있겠지요. 따라서 스핀의 x성분을 재면 두 가지 값을 모두 얻을 것입니다. 이제 x성분이 +1/2인 것들만 골라내어 마지막으로 다시 z성분을 재면 어떻게 되겠어요? 처음에 z성분이 +1/2인 것들만 골라내었고, 결국 z성분을 다시 재는 것이니까 당연히 +1/2만 얻어질 것 같아요? 그러나 실제로는 놀랍게도 +1/2인 것들과 -1/2인 것들이 섞여서 나옵니다.
이것이 양자역학의 특별한 점입니다. 고전역학에서처럼 생각하면 스핀의 z성분과 x성분 값이 각각 +1/2 및 -1/2이 가능하므로 모두 네 가지 상태가 있을 수 있고 그렇다면 위의 경우에 마지막으로 남는 양성자들은 두 성분이 모두 +1/2인 것들이겠지요. 그러나 양자역학에서는 스핀 성분 값이 그렇게 미리 정해져 있는 것이 아닙니다. 위에서 두 가지가 섞여 있다고 표현했지만 정확하게는 두 가지 상태가 포개져 있다는 뜻입니다.
예로서 x성분이 +1/2인 것이란 사실은 고유값이 +1/2인 x성분의 고유상태를 뜻하고, 이는 z성분을 보면 두 가지 고유상태, 곧 z성분의 고유값이 +1/2인 상태와 -1/2인 상태가 포개져 있는 상태에 해당합니다. 만일 도중에 x성분을 재지 않고서 바로 z성분을 다시 쟀다면 물론 +1/2 값만 얻었을 겁니다. 도중에 x성분을 측정했기 때문에 원래 z성분의 고유상태이던 계의 상태가 x성분의 고유상태로 변화한 거지요.
(매주 화, 목, 금 연재)



전체댓글 0