양자역학의 형식

[최무영의 과학이야기] <38> 양자역학 ③

개념과 기본원리가 있으면 개념들 사이의 관계를 설정해 주어야 합니다. 이론 체계에서 우리가 그것을 진술이라고 불렀습니다. 이른바 법칙이라 말하는 것인데 고전역학에서는 이것이 바로 뉴턴의 운동 법칙 또는 해밀턴의 원리 ― 뉴턴의 고전역학과 내용은 같지만 모양을 바꾼 것 ― 이지요. 이를 통해서 위치와 속도를 구할 수 있습니다. 사실 운동의 법칙 자체로는 가속도가 구해지지만 그것을 적분해서 속도와 위치를 구할 수 있지요.

마찬가지로 양자역학에서 상태를 기술해주는 상태함수가 만족하는 방정식이 있겠네요. 뉴턴의 운동방정식에 해당하는 방정식이 있습니다. 이른바 슈뢰딩거방정식(Schrödinger's equation)입니다. 양자역학의 형성에 가장 중요한 역할을 한 사람인 슈뢰딩거(Erwin Schrödinger)가 제안한 것으로 다음과 같이 쓸 수 있습니다.

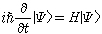
여기서 는 앞서 언급한 해밀토니안인데 고전역학에서는 대상의 에너지에 해당하지만 양자역학에서는 켓벡터에 작용해서 다른 켓벡터를 가져오는 이른바 연산자(operator)입니다. 위의 방정식은 추상적인 모양으로 주어져서 이해하기 어려울 텐데, 이를 질량 인 알갱이의 경우에 대해 구체적으로 1차원의 위치공간에서 나타내면

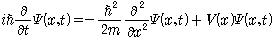
로 쓸 수 있습니다.

오른쪽에서 상태합수를 두 번 미분하는 항은 알갱이의 운동에너지에 해당하고 v(x)는 잠재에너지를 뜻합니다. 왼쪽에서 i는 다름이 아니라 허수(imaginary number), 곧

입니다. 고등학교 때 허수, 그리고 실수(real number)와 허수가 합쳐진 복소수(complex number)를 배웠지요? 허수는 실제로 없는 수인데 왜 배우는지 이상하다고 생각했을지 모르지만, 놀랍게도 허수는 자연현상을 기술할 때 필요한 것입니다. 이런 의미에서사실 허수도 존재한다고 할 수 있습니다. 위의 방정식은 허수부분(imaginary part)을 지니고 있으므로 이를 만족하는 풀이로서 상태함수도 허수부분을 지닐 수 있어서 일반적으로 복소수로 주어집니다.

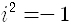
슈뢰딩거방정식은 이른바 편미분방정식의 형태를 갖고 있어서 좀 고약합니다. 뉴턴의 운동방정식은 간단해 보이지만, 가속도라는 것이 위치를 시간으로 두 번 미분한 것이므로, 사실은 미분방정식의 형태를 가지고 있지요. 뉴턴의 운동방정식을 풀어서 시간의 함수로 위치를 구할 수 있듯이 슈뢰딩거방정식을 풀면 상태함수

를 공간과 시간의 함수로 구할 수 있고, 이를 구하면 대상의 상태를 알았다고 말하는 것입니다.

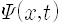
그런데 위의 슈뢰딩거방정식은 파동을 기술하는 방정식과 수학적으로 모양이 아주 비슷합니다. 그래서 이를 슈뢰딩거의 파동방정식(wave equation)이라고도 부르고, 그 풀이인 상태함수를 파동함수라고 부르기도 하는 것입니다. 전자 같은 물질알갱이가 파동의 성격을 갖고 있다고 했는데, 이는 전자의 상태를 기술하는 상태함수가 파동방정식을 만족하기 때문에 당연하다고 하겠습니다.

그러면 상태함수 또는 파동함수의 물리적 의미는 무엇일까요? 어떻게 대상의 상태를 나타낼까요? 일반적으로 상태함수의 절대값을 제곱하면 확률이 됩니다. 예를 들어 전자의 상태함수의 절대값을 제곱하면 그 전자가 주어진 순간 주어진 위치에 있을 확률이 얼마인지 알려주는 것입니다. 이러한 해석 규칙은 보른이 확립했다고 하지요.

이는 고전역학과는 완전히 다른 새로운 구조입니다. 고전역학에서 진술에 해당하는 부분이 뉴턴의 운동 법칙 또는 운동방정식입니다. 양자역학에서는 슈뢰딩거방정식이지요. 그런데 고전역학에서 내용은 같은데 형식을 바꾸어서 뉴턴의 운동방정식 대신에 해밀턴의 최소작용의 원리를 쓸 수 있다고 지적했습니다.

마찬가지로 양자역학도 내용은 같으면서 형식을 바꿀 수 있습니다. 그래서 슈뢰딩거방정식으로 주어지는 슈뢰딩거의 양자역학 형식과 본질은 같으나 모양이 다른 것으로 하이젠베르크가 만든 양자역학 형식이 있습니다. 슈뢰딩거방정식은 수학적으로는 편미분방정식인데 놀랍게도 이런 편미분방정식으로 주어진 진술을 행렬로 바꾸어서 나타낼 수가 있습니다. 그러니까 편미분방정식을 푸는 대신에 행렬 계산을 해도 똑같은 결과를 얻을 수 있습니다. 하이젠베르크를 비롯해서 보른과 조단(Pascual Jordan)은 이같이 행렬을 이용한 양자역학을 만들었고, 이를 행렬역학(matrix mechanics)이라고 부릅니다. 이에 반해 슈뢰딩거방정식은 파동방정식의 형태를 갖고 있으므로 슈뢰딩거의 형식은 파동역학(wave mechanics)이라고 부르지요.

그런데 이것으로 끝이 아니고 양자역학의 또 다른 형식이 있습니다. 이른바 길을 따라 적분하는 방법을 가지고 양자역학을 할 수 있다는 것으로 파인만(Richard P. Feynman)이 제안한 것입니다. 파인만은 들어본 학생 많죠? 타계한 지 오래지 않은 비교적 현대의 사람입니다. 장난꾸러기 같은 행동으로 널리 알려져 있는데, 디랙은 다소 폄하하는 뜻으로 '영리한 미국 소년(clever Yankee boy)'이라고 불렀다고 합니다.

고전역학에서 해밀턴의 원리 기억나나요? 대상 물체가 처음 시각

에 어떤 위치

에 있다가 나중 시각

에 다른 위치

로 갈 때 가능한 길이 일반적으로 매우 많을 것입니다. 그런데 그 중에서 어떤 길을 따라 가지요? 수많은 길 중에 실제로는 작용이 최소인 길을 따라간다고 했습니다. 이것이 바로 해밀턴의 최소 작용 원리이고, 뉴턴의 운동 법칙을 다르게 표현한 고전역학의 핵심입니다.

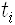
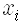
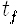
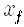
파인만의 방법은 고전역학을 기술하는 이러한 해밀턴의 원리를 양자역학도 기술하도록 확장한 것입니다. 이 방법에서는 작용 S의 지수함수로 주어진

를 처음 위치

에서 나중 위치

까지 가는 모든 길(경로; path)에 대해 더하면 상태함수에 해당하는 것을 얻게 됩니다. 수학적으로는

를

에서

까지 가는 길을 따라 적분하므로 이를 길적분(path integral)이라 부릅니다. 여기서 i는 물론 허수이고 작용 S는 고전역학에서 해밀턴의 원리에서와 마찬가지로 정의됩니다.

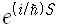
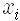
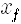
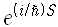
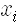
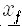
그런데 흥미롭게도 여기서 플랑크상수 H가 아주 작다면 대부분의 길을 따라 움직일 때 S/h가 매우 급격히 변하므로 적분하면 사실상 0이 되어버립니다. 다만 작용이 가장 작은 길만 살아남아서 적분에 기여하게 되지요. 결국 h -> 0의 극한을 택하면 최소 작용의 길만 살아남게 되는데, 이는 바로 해밀턴의 원리이네요.

일반적으로 플랑크상수 h가 무한히 작아지면 양자역학이 바로 고전역학으로 환원된다는 것을 보일 수 있습니다. 길적분에서 뿐만 아니라 행렬역학이나 파동역학에서도 플랑크상수가 작아지면 양자역학의 모든 결과가 고전역학의 결과와 똑같아진다는 것을 보일 수 있습니다.

따라서 고전역학이라는 체계가 틀린 것이 아닙니다. 고전역학은 아주 훌륭한 이론인데, 이에 대해 양자역학의 장점은 적용범위가 더 넓다는 것입니다. 말하자면 양자역학이 더 일반이론이고 고전역학을 포함한다고 할 수 있지요. 플랑크상수가 일상세계에 비하면 너무나 작기 때문에 우리 일상세계에서는 플랑크상수는 0이나 마찬가지이며, 따라서 일상세계와 같은 커다란 세계에서는 양자역학이 고전역학으로 완전히 환원됩니다.

그렇지만 분자나 원자와 같은 작은 세계에서는 상대적으로 플랑크상수가 작은 양이 아닙니다. 그럴 때는 양자역학이 고전역학과 다른 결과를 주며, 이 경우 양자역학이 고전역학보다 더 타당하다고 할 수 있습니다.

양자역학의 형식에는 위의 세 가지와 또 다른 확률적 형식(stochastic formulation)이라는 것이 있습니다만 여기서는 논의하지 않겠습니다.

(매주 화, 목, 금 연재)