그런데 20세기에 들어오면서 고전역학 체계로는 설명하기 어려운 현상들이 잇달아 발견되었습니다. 따라서 자연현상을 보다 정확하고 타당하게 기술하기 위해서 고전역학 체계에 대한 근본적인 재검토가 필요해졌습니다. 쿤의 표현을 빌리자면 비정상성 또는 변칙이 쌓였고, 이에 따라 고전역학에서 새로운 동역학 체계로 패러다임을 전환할 필요성이 생겨난 것입니다.
일반적으로 동역학에서는 대상을 서술하는 시간과 공간이 전제되어 있습니다. 뉴턴의 고전역학에서는 3차원 공간에 절대성을 지닌 시간이 따로 있는 고전적 시공간을 사용하였지요. 이러한 시간과 공간을 새롭게 인식하고 뉴턴역학에서 전제한 개념과 다르게 바꾸는 과정을 주도한 사람이 아인슈타인입니다.
그는 모든 기준틀은 동등하다는 전제, 이른바 상대성원리라는 기본가설로 출발했고, 이에 실험적으로 문제 됐던 빛의 빠르기가 언제나 일정하다는 원리를 덧붙여서 특수상대성이론을 제창했습니다. 나아가 이를 더 확장해서 가속기준틀도 포함한 기준틀, 곧 모든 관측자가 동등하다는 전제로서 일반상대성원리와 가속도는 중력과 본질적으로 같아서 한 가지로 해석할 수 있다는 등가원리로부터 출발해서 일반상대성이론을 만들어내었습니다.
한편 상대성이론과는 완전히 다른 의미에서 고전역학 체계가 만족스럽지 못하고 특히 원자나 분자 같은 작은 세계를 올바르게 기술할 수 없다는 것이 알려졌습니다. 이에 따라 시공간 문제와는 별도로 고전역학을 서술하는 양식 자체를 바꿔서 새로운 동역학 체계를 만들게 되었습니다. 이렇게 해서 고전역학보다 더 일반화된 이론으로서 양자역학이 만들어진 것은 상대성이론과 더불어 20세기에 일어난 과학혁명이라고 할 수 있는 중요한 사건입니다. 이번 시간에는 고전역학과 달리 새로운 서술 양식을 담고 있는 양자역학을 공부하겠습니다.
양자역학의 배경
고전역학은 원자나 분자 같은 작은 세계를 설명하는 데 합당하지 않았습니다. 대표적인 문제가 원자 중에 가장 간단한 수소 원자입니다. 원자 모형이 톰슨의 찐빵 모형에서 러더포드의 행성계 모형으로 바뀌게 된 과정을 앞에서 논의했는데, 이 러더포드의 모형에 의하면 수소 원자는 양성자 하나로 이루어진 원자핵이 가운데 있고, 주위에 전자가 하나 있습니다. 이들이 전기력으로 서로 당길 텐데, 끌려가지 않는 대신에 전자가 핵 주위를 돌고 있다고 생각합니다. 마치 지구가 중력에 의해서 원운동을 하므로 태양으로 끌려가지 않는 것처럼 전자도 원운동을 하고 있다는 것이지요.
그런데 여기에는 한 가지 문제가 있습니다. 전자가 이렇게 원운동을 하면 매우 빠르게 움직이게 됩니다. 원운동의 속도를 구할 수 있는데 우선 전자와 핵 사이의 거리를 아니까 전기력이 얼마나 되는지 알 수 있습니다. 거리가 약 0.5 Å이니까 2백억 분의 1미터입니다. 그러면 전기력이 얼마나 되는지 알고 전자의 질량도 아니까 얼마나 빨리 돌게 되는지 구할 수 있습니다. 마치 지구가 해 주위를 얼마나 빨리 도는지 구할 수 있듯이 말입니다. 계산해 보면 이 전자가 매우 빠른 속도로 도는 것을 알 수 있습니다.
그런데 전자는 전기를 띠고 있지요. 전기를 띤 알갱이가 움직이는 것을 전류라고 부릅니다. 따라서 전자가 원운동을 하면 동그란 고리 전류가 흐르는 것입니다. 이렇게 전류가 흐르게 되면 앞에서 얘기했듯이 전기마당뿐 아니라 자기마당도 생겨납니다. 전자는 원운동을 하므로 공간의 한 지점에서 전기마당이 일정하지 않고 시간에 따라서 변하게 됩니다. 그러면 전기마당이 변하면서 자기마당을 만들고 자기마당이 변하면서 전기마당을 만들어 서로 번갈아 생겨나면서 퍼져나가는 전자기파를 만들어냅니다.
이것을 정확하게 수학적으로 나타내는 식이 앞에서 논의한 맥스웰의 방정식입니다. 방정식의 수학적 의미를 우리가 이해할 필요는 없지만 맥스웰의 네 가지 방정식을 연립해서 풀면 전기마당과 자기마당이 변하면서 전자기파를 만들고 이것이 퍼져나간다는 것을 수학적으로 보여줄 수 있습니다. 결국 무슨 얘기냐면 수소 원자의 경우에 러더포드 모형을 받아들인다면 전자가 돌면서 계속 전자기파를 방출해야 한다는 것입니다. 전자기파라는 것은 바로 빛이고 에너지를 가지고 있습니다. 따라서 전자기파를 방출한다는 것은 에너지를 방출한다는 것입니다. 에너지를 방출하면 어떻게 될까요? 전자가 돌다가 에너지를 계속 내보내면 전자의 에너지가 줄게 되겠지요.
인공위성과 비교해보지요. 지표면에서 인공위성을 쏘아 올리면 처음에는 잘 돌겠지요. 그러나 어느 정도 높이로 쏘아 올려도 대기가 조금은 있으니까 공기 저항 때문에 에너지를 조금씩 잃어버리게 됩니다. 인공위성이 에너지를 잃어버리면 결국 수명을 다하게 되어서 떨어져 버립니다. 고도가 낮아지면 대기가 훨씬 빽빽하므로 공기 저항이 매우 크지요. 따라서 인공위성의 에너지는 열로 바뀌고 다행히 우리 머리 위로 떨어지기 전에 타버리게 됩니다. 마찬가지로 전자가 에너지를 잃어버리면 계속 돌지 못하고 원자핵에 달라붙게 될 겁니다. 결론적으로 말해서 러더포드의 모형을 따르면 원자는 계속 유지될 수 없습니다.
러더포드의 모형에는 또 다른 문제가 있습니다. 전자가 점점 에너지를 잃어버리는 만큼 전자기파, 곧 빛을 내비치므로 그 에너지도 아무런 값이나 다 가질 수 있어야 합니다. 빛의 에너지는 진동수가 높을수록, 곧 파길이가 짧을수록 크지요. 무지개의 빛을 보면 빨간빛과 보랏빛 중에 보라가 파길이가 짧으므로 에너지가 더 높습니다. 빛깔이란 빛의 파길이의 차이인데 이는 결국 에너지와 관련이 있지요. 아무튼 연속적으로 에너지를 잃어버리게 되니까 연속적인 파길이를 지닌 빛을 내비칠 수 있어야 합니다. 그런데 실제로 원자들이 내는 빛을 조사해보면 놀랍게도 어떤 특정한 파길이의 빛만을 내비칩니다. 파길이 별로 나눈 빛띠(spectrum)를 살펴보면 무지개처럼 이어져 있지 않고 띄엄띄엄하게 몇 개의 선들로 이루어져 있습니다. 예를 들어 질소는 주로 주황빛을 내고, 수은은 청록빛, 나트륨은 노란빛 등으로 정해져 있습니다. 원자가 연속적인 빛띠를 보이지 않는다는 사실은 러더포드의 모형에 잘못이 있음을 말해 줍니다.
원자 모형에 더해서 20세기 초에 문제가 됐던 것이 물질의 이중성(duality)이라는 것입니다. 예전엔 빛을 파동이라고 생각했습니다. 말 그대로 전자기파니까요. 실제로 빛은 장애물이 있으면 돌아가는 에돌이나 두 줄기 빛이 만날 때 위상차에 따라 강해지기도 하고 약해지기도 하는 간섭 등 파동의 독특한 성질을 보입니다. 그런데 20세기 들어와서는 빛이 어떤 경우에는 파동이 아니라 알갱이 같은 성질을 가진다는 사실을 알게 됐습니다.
빛이 알갱이 성질을 보이는 대표적인 현상으로 검정체내비침(흑체복사; black-body radiation)을 들 수 있습니다. 일반적으로 물질을 뜨겁게 하면 빛을 내비치지요. 이상적으로 빛을 내비치는 물체를 검정체(black-body)라고 합니다. 쉽게 생각해서 완전히 검은 물체라고 하지요.
요즘은 연탄을 거의 안 쓰니까 부지깽이라는 것을 보지 못했지요? 예전에는 연탄을 많이 썼는데 하루에 적어도 두 번은 연탄을 갈아줘야 했습니다. 불붙은 연탄 중에 많이 타버린 것을 부지깽이라는 쇠 집게로 집어서 옮겼습니다. 그런데 연탄에 부지깽이를 꽂아 놓으면 부지깽이가 뻘겋게 달구어지면서 빛을 냅니다. 어두운 데서도 빛을 내니까 보입니다. 백열전구도 보통 텅스텐으로 만들어진 실줄(filament)을 뜨겁게 가열해서 빛을 냅니다.
이처럼 물질을 뜨겁게 하면 빛을 냅니다. 물질의 에너지가 높아지니까 빛이란 형태로 에너지를 방출하는데, 이 때 빛이 완전히 파동이라면 이해할 수 없는 거동이 있습니다. 여기서 자세히 논의할 수는 없지만 파길이 별로 내비치는 빛의 세기를 맞출 수 없고 빛의 전체 에너지가 무한히 커지게 되는 등 문제가 생깁니다. 플랑크는 빛이 파동이 아니라 알갱이처럼 에너지를 지닌다고 생각해서 이러한 문제를 멋지게 해결하였고, 이에 따라 양자역학의 창시자라 인정을 받게 됩니다.
또한 앞에서 언급했지만 빛전자효과(광전효과)라는 것이 발견됐습니다. 이는 쇠붙이에 빛을 쬐면 전자가 튀어나오는 현상을 말하는데, 쇠붙이에 묶여 있던 전자가 빛을 받으면 에너지가 높아지니까 묶임을 끊고 도망 나오는 것입니다. 그것을 빛전자라고 하는데 나오는 거동을 보면 빛을 파동이라고 생각하면 설명할 수 없는 성질이 있습니다.
파동의 에너지는 일반적으로 떨기너비(진폭)가 클수록, 그리고 진동수가 높을수록 커집니다. 떨기너비는 파동의 세기를 의미합니다. 빛은 파길이와 진동수가 반비례하니까 파길이가 짧을수록 에너지가 커집니다. 파길이가 긴 빛을 쓰더라도 아주 강하게, 곧 떨기너비가 크게 쬐면 에너지가 충분히 많아지니까 전자가 나올 수 있어야 합니다. 그런데 실제로 실험에서는 파길이가 긴 빛은 아무리 세게 쬐어도 전자가 나오질 않습니다.
에너지를 많이 주어도 왜 전자가 나오지 않는지 설명하려면 빛에서 에너지가 파동에 실려 있지 않고 알갱이 하나하나가 가지고 다닌다고 해석해야 합니다. 이 빛전자효과의 이론을 처음으로 만든 사람이 아인슈타인입니다. 그것이 1905년이고 노벨상도 상대성이론이 아니라 바로 이 업적으로 받았습니다.
이에 더해서, 역시 앞에서 이야기했던 컴프턴효과가 관측되었습니다. 빛이 전자에 부딪치면 알갱이처럼 거동해서, 마치 당구공의 충돌과 똑같다는 것입니다. 당구공끼리 부딪쳤을 때와 마찬가지로 에너지와 운동량이 보존되며, 이는 빛의 알갱이, 이른바 빛알 하나하나가 에너지와 운동량을 지닌다는 것을 밝힌 것입니다.
빛알 하나의 에너지와 운동량은 빛의 진동수 v에 비례합니다. 에너지는
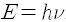
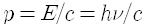
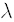
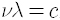
흔히 진동수 대신에 진동수에 2π 를 곱한 각진동수(angular frequency), 곧
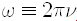
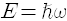
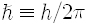
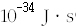
그렇다고 빛이 완전히 알갱이인가 하면 그것은 아닙니다. 빛이 에돌이하고 간섭을 하는 것을 봐서는 의심할 수 없는 파동입니다. 결국 빛은 파동의 성질도 가지고 알갱이의 성질도 가집니다. 두 가지 성질 중에 상황에 따라서 어느 한 가지가 나타나는 것입니다.
그래서 재미있는 생각을 하게 됐습니다. 파동인 줄로 알았던 빛이 알갱이의 성질을 갖고 있듯이 알갱이라고 생각했던 전자, 양성자, 중성자 따위도 파동의 성질을 갖고 있지 않을까 하는 생각을 한 것이지요. 이를 물질파(matter wave) 또는 드브로이 파동(de Broglie wave)이라 부릅니다. 이러한 가능성을 처음으로 생각한 프랑스의 드브로이(Louis de Broglie) 이름을 딴 것이죠. 그런데 프랑스에서 같은 철자를 '브로글리'라고 읽는 경우도 있어서 내가 아는 프랑스 물리학자에게 '브로이'가 확실한지 물어보았더니 잘 모르겠다고 하더군요. 자기 나라 글자를 어떻게 읽어야 할지 모른다니 어이가 없더군요. 서양 말과 달리 우리말과 글에는 이런 문제가 없지요. 아무튼 '브로이'가 맞는 듯합니다.
원래 물질파나 드브로이 파라고 하면 전자나 양성자 같은 물질 알갱이가 지니고 다니는 파동이라고 생각하였습니다. 그러나 사실은 물질 알갱이가 따로 있고 그것이 파동을 지니고 있는 것이 아니라 전자나 양성자 자체가 파동의 성질을 가졌다고 보는 것이 타당합니다.
이것을 실제로 확인하기 위해서 데이비슨(Clinton J. Davisson)과 저머(Lester H. Germer)가 전자의 에돌이 실험을 수행하였고 빛의 경우와 같은 결과를 얻었습니다. 전자도 빛과 마찬가지로 에돌이를 한다는 사실을 확인한 것이지요. 앞에서 논의했던 영의 겹실틈 실험에서 빛 대신에 전자를 써도 역시 간섭무늬를 얻게 됩니다. 전자 같은 물질 알갱이도 파동 성질을 지닌다는 이른바 파동-알갱이 이중성(wave-particle duality)이 확증된 것입니다.
파동-알갱이 이중성이란 언제나 파동과 알갱이의 성질을 같이 가졌다든지, 그 중간이라든지 하는 것이 아닙니다. 상황에 따라서 어떤 경우에는 파동처럼 거동하고 어떤 경우에는 알갱이로서 거동하는 것입니다. 예를 들어 겹실틈에 전자를 보내면 두 실틈 중에 어느 쪽으로 갈까요? 전자를 만 개쯤 보내면 대략 오천 개는 이쪽, 오천 개는 저쪽으로 갈 것 같습니다.
그런데, 각 전자가 어디로 가는지 확인해보기로 하겠습니다. 전자를 보내면서 두 실틈 중 어느 쪽으로 갔는지 눈에 불을 켜고 열심히 쳐다봅시다. 그러면 놀랍게도 간섭무늬가 사라집니다. 이렇게 위치를 측정하면 전자는 더 이상 파동의 성질을 가지지 않고 완전히 알갱이처럼 행동합니다. 그런데 위치를 측정하지 않으면, 다시 말해서 전자가 어디로 갔는지 쳐다보지 않으면 전자는 파동처럼 행동하는 것입니다. 우리가 측정하면 각 전자는 이리나 저리 둘 중에 한 쪽으로 갔습니다. 그러나 쳐다보지 않으면 파동처럼 거동해서 이리로도 가고 저리로도 간 것입니다. 강조하는데 '우리가 측정하지 않았기 때문에 모를 뿐이고 실제로는 어느 한 쪽으로 간 것이다'가 아니지요.
이것을 다음과 같이 비유합니다. 겨울 스키장에서 누군가 스키를 타고 내려온 자국이 있습니다. 두 발로 타니까 눈에 나란히 두 짝의 스키 자국이 나 있습니다. 내려오다 보니 높은 고목나무가 하나 있네요. 그런데 눈에 스키 자국이 나무 양 옆으로 한 짝씩 나 있습니다. 이 사람은 나무 어느 쪽으로 지나간 걸까요? 지나갈 때 보았다면 어느 한 쪽으로 지나갔겠지요. 그러나 보지 않았다면 양쪽으로 지나가서 다시 합쳐진 셈입니다. 이것이 이제 논의할 양자역학의 관점입니다.
(매주 화, 목, 금 연재)



전체댓글 0