상대성이론은 현대 사회에 커다란 영향을 끼쳤습니다. 과학과 직접 관련된 분야는 새삼 말할 필요가 없지만 철학 등 인문학과 사회과학, 그리고 예술에까지도 많은 영향을 주었습니다. 그래서 앞에서 언급했듯이 20세기에서 가장 중요한 사람으로 정치가나 군인이 아닌 아인슈타인이 선정된 것입니다.

|
남은 시간 동안 상대성이론과 관련된 예술에 대해 이야기하지요. 위 그림 9는 에셔(Maurits C. Escher)의 판화인데 제목이 바로 ≪상대성(Relativity)≫입니다. 보다시피 똑바로 볼 때는 말 그대로 위쪽이 위인데 고개를 왼쪽으로 기울여서 보면 왼쪽이 위입니다. 어느 쪽이 위냐 아래냐 하는 것이 상대적이라는 것을 보여 주고 있습니다. 특정한 관측자가 절대적이지 않다는 개념을 잘 보여주고 있지요.
다음 그림 10은 피카소의 작품으로 ≪아비뇽의 처녀들(Les Demoiselles d'Avignon)≫이라는 매우 유명한 그림입니다. 입체파(cubism)의 시작을 알리는 그림이라고 말하지요. 피카소는 아인슈타인과 같은 세대로서 본인이 상대성이론을 이해하고 있었다고 보기는 어렵지만 상대성이론에 대해 많이 들었으리라 추정합니다. 그 당시 파리에서 피카소가 가깝게 지내고 자주 토론했던 사람들 중에 상대성이론을 잘 알고 있던 사람이 있었다는 사실은 잘 알려져 있습니다.

|
이 그림을 보면 어떤 생각이 들어요? 이 정도는 나라도 그리겠다, 나라면 더 잘 그리겠다는 그런 생각이 들죠. 그런데 어린애는 책상을 보통 어떻게 그리지요? 책상 다리가 네 개 있지만 안쪽에 있는 다리는 잘 안 보입니다. 어른들은 보이는 대로 그리니까 보이지 않는 안쪽의 다리는 그리지 않는데 어린애들은 그것을 옆으로 튀어 나오게 그려서 있는 것을 확실하게 보여줍니다. 이는 한 점에서 보이는 대로 그린 것이 아니라 여러 점에서 본 것을 종합해서 그린 겁니다. 위의 그림도 어린애들이 그리듯이 여러 방향의 시각을 갖고 본 것입니다. 시점을 한 점으로 고정시켜서 그린 것이 아니라는 뜻이지요.
피카소가 처음부터 이렇게 그린 것이 아닙니다. 젊을 때의 작품은 사실적인 그림이 많은데 후대로 가면서 추상적인 그림을 그렸습니다. 왜 어린아이처럼 그리느냐고 묻자 피카소는 "이렇게 어린아이처럼 그리는 데 50년이 걸렸다"고 대답했다고 합니다. 50년 동안 공부를 한 후에야 비로소 사물의 본성을 그릴 수 있게 됐다는 겁니다.
그 전까지 서양미술의 주류는 사물을 그리는 데 원근법을 이용합니다. 먼 것은 작게 그리고 가까운 것은 크게 그리는데, 멀리 있는 것이 실제로 작은 것은 아니니까 이는 사실 눈속임이라 할 수 있습니다. 따라서 피카소는 원근법으로는 사물의 진정한 본성을 표현할 수 없다고 믿었습니다. 보는 시점을 한 군데로 고정시키지 않고 여러 군데에서 보아야 사물의 진정한 본성을 표현할 수 있다고 생각했지요. 상대성이란 개념이 느껴지는 듯합니다. 이에 따라 여러 화점에서 관찰하고 이를 재구성해서 표현한 작품이 바로 위의 그림입니다.
서양은 워낙 미개했기 때문에 20세기 들어와서야 이러한 의미를 생각했지만 동양은 훨씬 앞섰습니다. 조선시대의 화가 겸재 정선을 알죠? 그림11은 겸재의 ≪금강전도≫입니다. 보다시피 어느 한 지점에 화점을 놓고 그린 것이 아닙니다. 여러 군데의 화점에서 그렸지요. 이러한 한국화 기법을 삼원(三遠)이라고 하는데 높고(고원), 깊고(심원), 평평한(평원) 지점, 적어도 세 군데의 성격이 다른 화점을 잡아서 그립니다. 이렇게 해야 실제 본성에 가깝게 표현할 수 있다고 믿은 것입니다. 겸재 정선이 18세기 초에 그린 그림이니 피카소보다 이백 년 가량 앞섰네요.

|
프랑스 사람인 마티스(Henri Matisse)는 색채의 마술사라고 불리는 유명한 화가입니다. 야수파(Fauvism)로 알려져 있지요. 그림 12는 그의 ≪춤La Danse≫이라는 그림인데 조금 전에 봤던 피카소와는 뭔가 좀 다르죠. 그런데 이 그림은 뭔가 역동적인 느낌이 듭니다. 왜 그런 느낌이 들까요? 보다시피 모두 손잡고 춤을 추는데 앞의 사람만 손이 떨어져 있습니다. 이것이 그림에 대칭을 살짝 깨는 강조점을 줘서 역동성을 느끼게 한다고 합니다. 손이 모두 붙어 있으면 정적 평형상태라는 느낌을 줄 수 있는데 떨어져 있어서 평형이 아니라는 느낌을 줍니다. 그러나 지금 강조하려는 것은 마티스가 피카소와 다른 점입니다.

|
아인슈타인보다 조금 이전 시대에 푸앵카레가 있었습니다. 푸앵카레는 역사상 가장 뛰어난 수학자 중 한 사람이고 동역학과 상대성이론의 기초를 닦은 사람인데 상대성이론을 만들지는 못했습니다. 수학으로 따지면 아인슈타인보다 훨씬 뛰어나다고 할 수 있습니다. 그런데 이 푸앵카레와 아인슈타인의 관계를 마티스와 피카소의 관계로 비유하기도 합니다.
그림 13은 피카소의 ≪게르니카Guernica≫라는 그림인데, 스페인의 학살을 그린 것입니다. 공화국이던 스페인에서 프랑코(Francisco Franco) 장군이 군사 쿠데타를 일으켜 정권을 탈취하자 시민들이 저항했고 이에 따라 쿠데타 세력과 공화파 시민 사이에 스페인 내전이 일어났습니다. 스페인 학살이란 내전 중에 파시스트(fascist) 프랑코를 지원하는 독일 나치(Nazi) 군이 게르니카 마을을 폭격해서 수백 명이 학살당한 사건입니다. 우리나라의 노근리 학살이나 광주 학살이 생각나네요. 미국은 내전에 개입하지 않는다고 하고서는 양쪽에 무기를 팔아서 '국익'을 챙겼다고 합니다. 스페인 내전을 그린 작품으로 헤밍웨이(Ernest Hemingway)의 소설 ≪누구를 위하여 종은 울리나(For Whom the Bell Tolls)≫가 유명하고, 공화파 병사가 총에 맞아 죽는 순간을 포착한 카파(Robert Capa)의 충격적인 사진도 널리 알려져 있습니다. 최근에 우리나라에서도 전시했지요.

|
이 그림은 독재자 프랑코가 죽고 스페인이 민주화되자 비로소 피카소의 고국으로 돌아와서 마드리드의 미술관에 있습니다. 그런데 이를 걸개로 만든 작품이 미국 뉴욕의 국제연합 본부에 있는데 한동안 장막에 덮여 볼 수 없었다고 합니다. 그게 언제였냐면 미국이 이라크를 침략했을 때였습니다. 스페인 학살이 현대의 이라크 학살을 연상시키니까 그림을 못 보게 하려고 가린 거지요. 국제연합의 본질을 극명하게 보여주었습니다.
혹시 미국은 '선진국'이고 이라크 같은 곳은 문명이 뒤쳐져 있는 '후진국'이라고 생각한 적이 있습니까? 그건 지극히 잘못된 생각입니다. 이라크는 메소포타미아 문명, 곧 인류 최고 문명의 발상지며 그런 역사를 계속 가져 왔습니다. 반면에 미국이라는 나라는 문화랄 것이 전혀 없는 나라입니다. 백인들이 원주민을 잔인하게 대량 학살하고 나서 미국을 만든 것이 기껏해야 200년이 조금 넘었습니다. 미국이야말로 출발부터 야만의 나라고 이라크는 도리어 문화의 나라라 할 수 있겠습니다.
그런데 한국의 정치, 문화, 교육, 언론 등에서는 모든 것을 미국의 시각에서 마치 원근법처럼 미국은 크게 그리고 이라크는 아주 멀게 느껴지도록 조그맣게 그리는 것입니다. 사실 우리나라는 이런 원근법의 속임수에서 60년을 살아온 것입니다. 지금도 그렇지요. 원근법에서 해방돼야 한다고 주장한 것이 바로 입체파이고 피카소가 이러한 관점에서 스페인의 학살을 직접적으로 표현한 것이 ≪게르니카≫입니다.

|
다음 그림 14도 피카소의 그림인데, 등장인물이 낯익고, 어디서 본 듯한 얼굴이지 않아요? 제목이 ≪한국에서의 학살(Massacre in Korea)≫입니다. 한국전쟁 때 황해도의 신천리에서 벌어진 학살을 그린 것입니다.
오른쪽의 흉악한 괴물같이 보이는 것이 미국과 남한의 군인들이고 왼쪽이 신천리 주민들입니다. 제대로 알려져 있지 않지만 수만 명이 학살당했다고 합니다. 신천리가 조그마한 마을이니까 사실상 주민 전부를 죽인 것일 테고, 이에 비하면 게르니카는 아무 것도 아니지요. 피카소가 1951년 소식을 듣고 격분해서 그렸다고 하는데 남한에서는 이 그림 자체가 철저히 금지됐습니다. 세상이 나아져서 요즘은 이렇게 볼 수 있지요. 여러분은 박정희 정권의 유신시대가 얼마나 공포와 죽음의 세계였던지 이해할 수 없을 것입니다. 그에 비하면 광주 학살에도 불구하고 전두환 정권 시대가 차라리 나았지요. 아무튼 이 그림은 프랑스 파리의 피카소 박물관에 있으니 기회가 되면 보기 바랍니다.

|
위 그림 15는 에셔의 ≪파충류reptile≫이라는 판화입니다. 2차원의 그림인데 도마뱀이 조금씩 생겨나서 그림에서 나오고 위로 올라가서 존재의 기쁨을 만끽하느라 숨을 크게 한 번 내쉬고, 다시 그림으로 들어갑니다.
이것은 2차원 세계에서 한 차원을 높여서 3차원으로 나오려고 하는 존재의 몸부림을 그린 것입니다. 결국 2차원의 화폭에 어떻게 3차원을 표현할지가 과제인데 이를 상징적으로 표현한 것입니다. 이는 입체파에서도 중요한 의미이지요. 상대성이론에서 3차원의 공간에다 시간을 더 붙여서 4차원 시공간으로 올라가는 것을 비유하는 듯합니다.
혹시 ≪평평한 나라 (Flatland:A Romance of Many Dimensions)≫라는 소설을 아는 사람 있어요? 교육자이자 신학자였던 애보트(Edwin A. Abbott)의 1884년 작품인데, 최근에 우리말로 ≪이상한 나라의 사각형≫이라는 제목으로 번역이 된 것 같습니다. 공간의 차원에 대해 기술한 상당히 통찰력이 있는 소설로서, 평평한 나라, 곧 2차원 세계의 존재에 관한 이야기입니다. 도형으로 나타내어 변이 많을수록 지위가 높은데, 지식층 또는 중간계급이라 할 사각형이 말하는 형식으로 되어 있지요. 이 나라의 사회 구성을 기술하고, 1차원 직선나라에 대해 고찰하는가 하면 3차원 공간나라에서 존재하는 공의 방문을 맞기도 합니다. 그저 공상과학이라기보다 공간의 차원과 관계되어 정확한 수학적 기술을 보여주지요. 더욱이 여성과 계급의 문제 등 핵심적인 사회비판적 요소도 지닌 훌륭한 작품입니다.

|
그림 16도 에셔의 작품으로 ≪되비침공을 든 손(Hand with Reflecting Sphere)≫인데 유리구슬을 손에 들고서 보는 것입니다. 자신의 얼굴이 보이네요. 보다시피 이 조그마한 구 안에 뒤의 모든 것이 다 들어 있습니다. 평면거울이면 자기 얼굴만 보고 배경은 다 보지 못할 터인데 구면 거울이기 때문에 먼 공간도 구부려서 보여줍니다. 일반상대성이론에서 굽은 공간을 보여주는 듯합니다.
그림 17 역시 에셔의 작품으로 왼쪽 ≪동그라미 극한(Circle Limit IV)≫은 앞에서 얘기한 안장 모양 공간을 평면에 나타낸 것입니다. 마음에 따라서 악마를 볼 수도 있고, 천사를 볼 수도 있습니다. 악마와 천사가 반복되는데 가장자리로 갈수록 수가 엄청나게 많아집니다. 여기에 서로 만나지 않는 선, 곧 평행선을 얼마든지 많이 그을 수 있습니다. 퍼져나갈수록 공간이 훨씬 더 증가하는 안장 모양 공간을 보여줍니다. 수학에서 쌍곡선적 공간을 표현하는 푸앵카레 원반 모형(Poincaré disk model)을 예술로 표현한 것이지요.

|
오른쪽의 ≪더 작게 더 작게(Smaller and Smaller)≫ 작품은 반대입니다. 이건 가장자리로 갈수록 공간이 점점 줄어드는 것을 말하는 것입니다. 여기에 평행선을 그리면 필연적으로 만나게 됩니다. 공 겉면 같은 타원적 공간을 나타냅니다.
몇 가지 질문
혹시 질문 있어요?
학생: 중력이 시공간을 변화시켜 빛이 꺾인다고 하셨는데, 처음에 얘기했을 때는 중력이 질량이 있는 물질 사이에 작용하는 힘이라고 말씀하셨습니다. 빛에는 질량이 없는데도 중력이 영향을 끼치나요?
빛에는 질량이 없지만 중력이 작용합니다. 이는 빛이 최단거리, 이른바 측지선을 달리는데 중력이 있으면 시공간을 굽게 해서 측지선을 바꾸지요. 따라서 빛은 중력의 영향을 받습니다. 사실 측지선을 달린다는 것은 다른 알갱이들도 마찬가지지요.
학생: 그러면 중력이 질량과 질량 사이에 작용하는 힘이라고 정의할 수 없는 것인가요?
일반적으로 질량이란 정지해 있을 때의 질량, 곧 정지질량을 가리킵니다. 빛은 정지질량이 없으므로 이러한 면에서 보면 빛은 예외인 셈입니다. 사실 빛이 정지해 있는 기준틀이 존재하지 않습니다. 왜냐면 우리가 빛과 똑같이 갈 수가 없기 때문입니다. 빛과 똑같이 가는 기준틀이 없기 때문에 빛은 정지해 있을 수 없는 것입니다. 그것이 빛의 독특한 성질입니다. 그러나 빛은 에너지와 운동량을 가지고 있지요. 그러니 중력은 (정지)질량보다는 에너지와 운동량에 작용한다는 표현이 더 적절하다고 하겠습니다, 만일
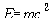
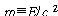
학생: 중력이 있으면 시공간이 굽고 빛의 경로가 굽는다고 하셨는데 빛이 전자기파니까 전자기파 자체가 굽는 것 아닌가요? 또, 그러면 전기장과 자기장 자체가 굽는다는 의미 아닌가요?
그렇습니다. 전자기파가 중력을 받아서 경로가 굽지요. 에너지와 운동량을 지닌다는 점에서 중력의 작용을 받는다고 할 수 있습니다. 그런데 전기마당과 자기마당이 중력마당과 어떤 관련이 있는가는 사실 매우 어려운 문제입니다. 일반상대성이론은 중력마당을 공간의 기하학적 성질로 귀착을 시켜 해석하였습니다. 이는 참 멋지고 성공적인 착상이었고, 따라서 전자기마당도 마찬가지로 공간의 기하학적 성질로 바꾸자고 생각했는데, 그것을 통일마당이론(unified field theory)이라고 불렀습니다. 이는 고전적인 마당이론으로서 아인슈타인을 포함한 많은 사람들이 시도했으나 성공적인 결과는 얻지 못했습니다. 그 후로는 양자마당이론의 관점에서 전자기상호작용에서 출발하여 약상호작용, 강상호작용과 함께 궁극적으로 중력상호작용까지 통합하여 기술하려 하지만 아직 해결하지 못하고 있습니다.
(매주 화, 목, 금 연재)



전체댓글 0