일반상대성이론에서 중력과 시공간을 맺어주는 관계를 마당방정식(field equation)이라 부릅니다. 유감스럽게도 일반상대론은 특수상대론과 달리 수학적으로 상당히 어렵습니다. 수학적 내용을 알 필요는 전혀 없지만 일반상대론의 핵심을 나타내는 '아름다운' 식이니 한 번 써보기나 하지요.
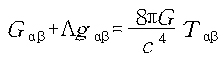
여기서 아래첨자가 붙은 기호는 텐서(tensor)라고 하는 물리량을 나타냅니다. 간단하게 크기만 지닌 스칼라와 차원 수만큼의 성분을 가진 벡터라는 양은 알고 있지요? 텐서는 조금 더 복잡한데 4차원에서는
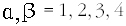
마당방정식에는 여러 텐서가 관계하는데
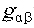
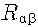
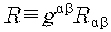
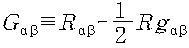
한편 오른쪽의
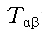
아, 여기서 람다(
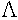
일반상대론 현상
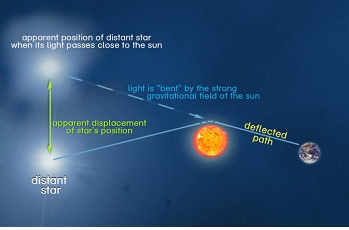
일반상대성이론의 마당방정식을 풀면 여러 가지 흥미로운 현상이 얻어집니다. 대표적인 것은 이미 지적한대로 중력마당에서는 빛이 똑바로 가지 않고 휘어져 가는 현상입니다. 아래 그림에서처럼 지구에서 보았을 때 해 뒤편에 별이 있으면 별빛이 오다가 해의 중력 때문에 휘어져서 지구로 들어옵니다. 따라서 지구에서는 별이 위쪽에 있는 것으로 보입니다. 해가 없다면 빛이 똑바로 오니까 별은 원래의 아래 위치로 보이지요. 결국 해에 의해서 별의 위치가 치우쳐 보이게 됩니다.
|
이를 보려면 별이 해 근처로 왔을 때 관측하면 되는데 보통 때는 햇빛 때문에 별이 보이지 않지요. 햇빛을 막을 수 있는 유일한 방법이 바로 개기일식입니다. 달이 해를 가려주니까 별빛은 들어올 수 있습니다. 그래서 에딩턴(Arthur S. Eddington)은 1919년 개기일식 지역이었던 아프리카의 한 섬에 가서 이를 측정했고 일반상대성이론의 예측만큼 치우쳐졌다는 것을 확인했지요. (사실은 에딩턴의 관측 자료는 그리 명확하지 않았고 일부를 선택했다고 합니다. 이른바 '인위적 실수'였는지도 모르겠네요.) 최근에는 멀리 떨어진 퀘이서(quasar)에서 나온 빛이 해의 중력에 의해 휘어지는 현상을 관측하여 훨씬 정밀한 결과를 얻었습니다.

|
이렇게 중력이 빛의 경로를 구부리면서 마치 렌즈와 비슷한 효과를 주므로 일반적으로 이러한 현상을 중력렌즈(gravitational lens)라고 부릅니다. 멀리 떨어져 있는 은하나 퀘이서에서 나온 빛이 다른 천체에 의해 경로가 굽어져서 지구로 오면 그 상이 그림 7 왼쪽 사진처럼 여러 개로 보이거나 때로는 오른쪽 사진처럼 가락지 모양으로 보이는 경우도 생겨납니다.
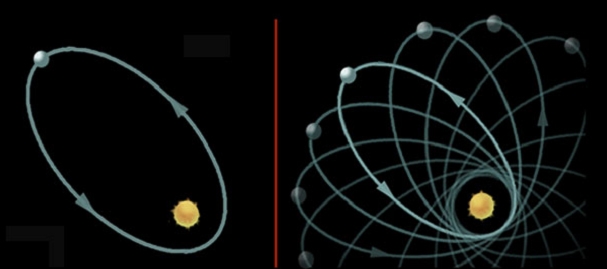
일반상대론은 또한 행성의 운동에 뉴턴의 고전역학과는 조금 다른 결과를 줍니다. 뉴턴 역학에 따르면 그림 8의 완쪽처럼 행성은 해를 초점으로 하는 타원 자리길을 따라 돕니다. 케플러의 법칙을 정확히 만족하죠. (그림 8은 매우 과장되게 타원을 그렸습니다. 실제로 대부분 행성의 자리길은 거의 원에 가깝습니다.) 그러나 일반상대론에 따르면 행성은 오른쪽 그림처럼 이른바 장미꽃 자리길을 그리며 움직입니다. (이것도 엄청나게 과장해서 그린 겁니다.) 따라서 자리길에서 태양에서 가장 가까운 지점이 움직여 가는 근일점 옆돌기(세차; precession of perihelion) 현상이 나타납니다.
사실 뉴턴 역학에서도 해와 행성이 하나만 있어야 자리길이 타원이 되고, 실제로는 다른 행성들의 영향과 춘분점 옆돌기 때문에 근일점 옆돌기가 나타나게 됩니다. 이러한 근일점의 움직임은 이미 관측되어 있었는데 뉴턴 역학의 요소로 설명할 수 없는 부분이 있었습니다. 이 부분이 100년에 43초인데 바로 일반상대론의 효과를 예측한 값과 잘 일치합니다. 각도 1도의 60분의 1이 1분이고 1분의 60분의 1이 1초인데 해마다 43초도 아니고 100년에 43초이니 매우 작은 효과이지요. 최근에는 이중 맥동성(binary pulsar)에서 이러한 옆돌기를 정밀하게 관측하였습니다.
|
그리고 일반상대론의 또 다른 결과로서 중력마당에서 빛이 나오면 에너지를 잃으므로 파길이가 길어지는 중력 빨강치우침(gravitational redshift) 현상을 보이고, 이와 관련해서 중력마당에서는 특수상대론에서처럼 시간도 천천히 흐르게 됩니다, 이를 중력 시간 늦춰짐(gravitational time dilation)이라 하는데 모두 정밀한 실험을 통해 확인이 되었습니다. 예컨대 비행기에 원자시계를 싣고서 비행하다가 착륙해서 지상의 시계와 비교하면 중력이 약했던 비행기에 있는 시계가 조금 빨리 갔음을 알 수 있습니다. 요새 온곳 위치잡기 체계(global positioning system; GPS)를 많이 이용하지요? 인공위성에 시계를 싣고서 위치를 추적하는데, 정밀하게 시간을 재기 위해서는 이러한 시간 늦춰짐 현상을 고려해야 합니다.
일반상대성이론의 중요한 의미는 결국 시간과 공간 자체도 동역학적인 양이라는 것입니다. 시공간이 먼저 주어져 있고 물질이 시공간에 존재해서 어떻게 하는 것이 아니라 물질이 시공간 자체를 변화시킵니다. 물질이 중력을 만들어서 시공간을 굽게 만드는 것입니다. 그런가 하면 거꾸로 시공간이 물질의 운동을 결정합니다. 시공간이 어떻게 굽었는지에 따라서 물질은 굽은 시공간에 맞춰져서 움직여 가는 것뿐입니다. 마치 산이 많으면 물이 교묘하게 잘 돌아서 가듯이 시공간이 굽어져 복잡하게 있으면 물질 알갱이들은 거기서 최단거리를 찾아서 갑니다.
따라서 물질이 시공간의 굽어진 곡률을 결정하고, 굽은 시공간이 물질의 운동을 결정하는 것입니다. 그런데 시공간이란 자체가 마당이고 마당은 에너지를 지니고 있습니다. 에너지는 또한 물질입니다. 질량과 에너지가 서로 왔다 갔다 할 수 있다는 것을 배웠으니까요. 이렇게 놓고 보면 결국은 시공간, 에너지, 물질 이런 것들이 모두 밀접하게 연결돼 있어서 그 전체가 자연의 본질을 이룬다는 것입니다. 따로따로 있는 것이 아니고 모두 얽혀있다는 사실을 일반상대성이론이 잘 보여 줍니다.
(매주 화, 목, 금 연재)



전체댓글 0