여기서 원리를 포기하는 대신에 중력이 시공간을 굽게 만든다고 해석할 수 있습니다. 우리가 알고 있는 시공간은 4차원이지요. 특수상대성이론에서는 가속도를 고려하지 않으므로 평평한 4차원의 시공간을 다룹니다. 그러나 가속도, 곧 중력을 다루는 일반상대성이론에서는 시공간이 중력에 의해 굽어져 있습니다. 이렇게 굽은 시공간(curved space-time)에서 물질 알갱이와 마찬가지로 빛은 최단경로를 따라서 움직인다고 생각합니다.
종래의 해석, 뉴턴의 해석에서는 시간과 별개로 3차원 공간은 언제나 평평합니다. 거기서 중력이 작용할 때 물체의 움직임은 뉴턴의 운동 법칙에 의해 기술됩니다. 곧 중력마당에 해당하는 가속도가 생기고, 그에 따라 각 순간마다 속도와 위치가 정해져서 물체의 경로가 결정되지요. 그래서 지표면에서 공을 던지면 지구 중력에 의해 포물선 경로를 따라 갑니다. 지구는 태양의 중력에 의해 타원 자리길(궤도)을 따라 움직입니다.
새로운 해석, 일반상대성이론에서는 모든 물체는 중력에 의해 굽어진 시공간에서 최단경로를 따라 갑니다. 공을 던지면 지구 중력을 받아 날아가는 것이 아니라 지구 중력 때문에 굽어진 시공간에서 최단경로를 따라 가는 것입니다. 이것이 우리에게는 포물선으로 보이지요. 지구도 태양의 중력 때문에 굽어진 시공간에서 단지 최단경로를 가는데 그것이 우리에게는 타원 자리길로 보이는 것입니다. 결국 중력을 바깥에서 주어진 힘, 외부적인 요인이 아니라 바로 공간 자체의 기하학적 성질로 보는 거지요. 이는 참으로 놀랍고 멋진 해석입니다.
그런데 굽은 공간에서 최단경로는 어떻게 주어질까요? 4차원 시공간은 평평하더라도 그릴 수 없고 상상하기도 어려우니 간단하게 2차원 공간, 곧 면에서 생각해보지요. 평평한 2차원 공간이란 바로 평면을 말합니다. 그런데 우리가 살고 있는 지구의 겉면은 평면이 아니라 구면이니 바로 굽은 면입니다. 서울에서 다른 나라로 빨리 가려면 어떻게 가야 할까요? 지구를 꿰뚫지 않고 지표면에서 가는 경우에 최단경로는 지구의 대원을 따라가는 것입니다. 그것을 측지선geodesic이라고 부릅니다. 항공로가 대체로 측지선을 따라 갑니다. 정치, 경제적인 문제로 어떤 나라의 영공을 지나가지 못해서 돌아가는 수도 있겠지요.
이러한 굽은 공간에서 기하학(geometry)은 어떻게 될지 생각해봅시다. 일반적으로 두 점을 최단거리로 연결하는 선을 직선이라 합니다. 주어진 직선 밖의 한 점을 지나서 이 직선에 평행한 직선은 딱 하나만 있다는 얘기 잘 알지요? 이 명제는 분명히 맞습니까? 언제나 참인가요?
사실 이것은 아무리해도 증명할 수 없습니다. 물리에서 가설, 기본원리에 해당하는 것인데 수학에서는 보통 공리(axiom) 또는 공준이라고 부릅니다. 증명할 수는 없지만 옳다고 생각하고 시작하자는 거지요. 평행선이 딱 하나 존재한다고 전제하면 여러 가지 성질을 이끌어낼 수 있는데 그것이 바로 유클리드 기하학(Euclidean geometry)이라고 부르는 ― 그동안 여러분이 배웠던 ― 기하학입니다. 이런 기하학에서는 세 직선으로 이루어진 삼각형의 내각의 합이 180도가 되고 한 점에서 거리가 같은 점의 집합, 곧 동그라미를 그리면 원둘레와 지름의 비, 원주율이 파이(π = 3.141592…)가 되지요.
그런데 이와 다르게 시작해 봅시다. 주어진 직선 밖의 한 점을 지나서 그 직선에 평행한 직선이 무수히 많다고 생각해봅시다. 이 주장이 틀렸다고 아무도 증명하지 못하니 걱정하지 말고 우겨도 됩니다. 그렇게 출발해서 논리를 전개하면 완전히 다른 공간의 성질을 얻게 되는데 이를 쌍곡선적 기하학(hyperbolic geometry), 또는 19세기 초에 이를 만들어낸 수학자 볼리아이(János Bolyai)와 로바체브스키(Nikolai I. Lobachevsky)의 이름을 따서 볼리아이-로바체브스키 기하학이라 부릅니다.
|
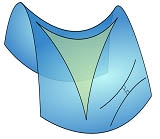
이러한 공간을 2차원 면으로 나타내면 그림 4처럼 안장(saddle) 모양이 됩니다. 이는 평면이 아니고 보다시피 가운데는 좁고 양쪽 가장자리로 갈수록 넓어지기 때문에 무수히 많은 평행선을 그을 수 있습니다. 평행선이라는 것은 양쪽으로 아무리 연장해도 서로 만나지 않는 직선들을 평행선이라고 하니까요. (여기서 직선이라는 것은 언제나 측지선, 곧 면을 따라서 두 점 사이 최단거리를 주는 선을 말하는 것입니다.) 이러한 면에 삼각형을 그리면 홀쭉해 보이는 모양이 돼서 그 내각의 합이 180도보다 작습니다. 그리고 동그라미를 그리면 원주율은 파이(π)보다 커집니다.
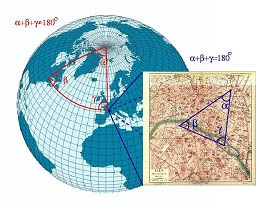
뒤이어 19세기 중반에는 리만(G.F. Bernhard Riemann)이라는 위대한 수학자가 거꾸로 평행선이란 하나도 없다고 전제하고 리만기하학(Riemannian geometry)이라고도 불리는 새로운 타원적 기하학(elliptic geometry)을 만들었습니다. 그것은 2차원에 비유하자면 바로 공의 겉면과 같은 것입니다. 지구에서 지표면을 따라서 평행선을 그릴 수 있나요? 대원을 따라 선들을 그으면 결국 어디서든 서로 만나게 됩니다. 여기에 삼각형을 그리면 어떻게 될까요? 그림 5처럼 삼각형이 뚱뚱한 모양으로 되니까 내각의 합 가 180도보다 커질 것이 명백합니다. 그리고 동그라미를 그리면 원주율은 파이보다 작아지지요. 극단적으로 적도라는 동그라미를 생각하면 지표면을 따라 재는 지름은 적도의 반이지요. 따라서 원주율은 2가 되어서 파이보다 작네요.
|
이러한 쌍곡선적 기하학과 타원적 기하학을 총칭해서 비유클리드 기하학(non-Euclidean geometry)이라고 부릅니다. 이는 평평한 공간에서 성립하는 유클리드 기하학과 달리 굽은 공간을 기술합니다. 리만은 이러한 모든 공간을 계량(metric) 및 곡률(curvature), 곧 굽음의 정도를 써서 일반적으로 기술하였으므로 넓은 의미에서 리만기하학은 모든 비유클리드 기하학을 가리킵니다.
결국은 우리의 우주는 중력이 존재하지 않으면 유클리드 기하학이 성립하는 평평한 4차원 시공간, 정확히는 민코프스키 시공간일 터인데 여기저기 물질이 존재하므로 중력마당을 형성하였고, 따라서 굽어진 시공간이 되고 비유클리드 기하학이 성립할 겁니다. 구체적으로 어떤 모습인가는 흥미로운 문제지요. 우리 우주는 이를테면 쌍곡선적일까요, 아니면 타원적일까요?
(매주 화, 목, 금 연재)



전체댓글 0